posttest only experimental design

Request consultation

Do you need support in running a pricing or product study? We can help you with agile consumer research and conjoint analysis.

Looking for an online survey platform?

Conjointly offers a great survey tool with multiple question types, randomisation blocks, and multilingual support. The Basic tier is always free.

Research Methods Knowledge Base

Navigating the Knowledge Base
Foundations
Measurement
Research Design
Conclusion Validity
Data Preparation
Descriptive Statistics
Dummy Variables
General Linear Model

Posttest-Only Analysis

Factorial Design Analysis
Randomized Block Analysis
Analysis of Covariance
Nonequivalent Groups Analysis
Regression-Discontinuity Analysis
Regression Point Displacement
Table of Contents

To analyze the two-group posttest-only randomized experimental design we need an analysis that meets the following requirements:

has two groups
uses a post-only measure
has two distributions (measures), each with an average and variation
assess treatment effect = statistical (i.e. non-chance) difference between the groups

Before we can proceed to the analysis itself, it is useful to understand what is meant by the term “difference” as in “Is there a difference between the groups?” Each group can be represented by a “bell-shaped” curve that describes the group’s distribution on a single variable. You can think of the bell curve as a smoothed histogram or bar graph describing the frequency of each possible measurement response. In the figure, we show distributions for both the treatment and control group. The mean values for each group are indicated with dashed lines. The difference between the means is simply the horizontal difference between where the control and treatment group means hit the horizontal axis.

Now, let’s look at three different possible outcomes, labeled medium, high and low variability. Notice that the differences between the means in all three situations is exactly the same. The only thing that differs between these is the variability or “spread” of the scores around the means. In which of the three cases would it be easiest to conclude that the means of the two groups are different? If you answered the low variability case, you are correct! Why is it easiest to conclude that the groups differ in that case? Because that is the situation with the least amount of overlap between the bell-shaped curves for the two groups. If you look at the high variability case, you should see that there quite a few control group cases that score in the range of the treatment group and vice versa. Why is this so important? Because, if you want to see if two groups are “different” it’s not good enough just to subtract one mean from the other – you have to take into account the variability around the means! A small difference between means will be hard to detect if there is lots of variability or noise. A large difference will between means will be easily detectable if variability is low. This way of looking at differences between groups is directly related to the signal-to-noise metaphor – differences are more apparent when the signal is high and the noise is low.

With that in mind, we can now examine how we estimate the differences between groups, often called the “effect” size. The top part of the ratio is the actual difference between means, The bottom part is an estimate of the variability around the means. In this context, we would calculate what is known as the standard error of the difference between the means. This standard error incorporates information about the standard deviation (variability) that is in each of the two groups. The ratio that we compute is called a t-value and describes the difference between the groups relative to the variability of the scores in the groups.

There are actually three different ways to estimate the treatment effect for the posttest-only randomized experiment. All three yield mathematically equivalent results, a fancy way of saying that they give you the exact same answer. So why are there three different ones? In large part, these three approaches evolved independently and, only after that, was it clear that they are essentially three ways to do the same thing. So, what are the three ways? First, we can compute an independent t-test as described above. Second, we could compute a one-way Analysis of Variance (ANOVA) between two independent groups. Finally, we can use regression analysis to regress the posttest values onto a dummy-coded treatment variable . Of these three, the regression analysis approach is the most general. In fact, you’ll find that I describe the statistical models for all the experimental and quasi-experimental designs in regression model terms. You just need to be aware that the results from all three methods are identical.

y i is the outcome of the i th unit
β 0 = coefficient for the intercept
β 1 = coefficient for the slope
z i = 1 if i th unit is in the treatment group, = 0 if i th unit is in the control group
e i = residual for the i th unit

OK, so here’s the statistical model in notational form. You may not realize it, but essentially this formula is just the equation for a straight line with a random error term thrown in ei . Remember high school algebra? Remember high school? OK, for those of you with faulty memories, you may recall that the equation for a straight line is often given as:

which, when rearranged can be written as:

(The complexities of the commutative property make you nervous? If this gets too tricky you may need to stop for a break. Have something to eat, make some coffee, or take the poor dog out for a walk.). Now, you should see that in the statistical model yi is the same as y in the straight line formula, b0 is the same as b , b1 is the same as m, and Zi is the same as x . In other words, in the statistical formula, b0 is the intercept and b1 is the slope.

It is critical that you understand that the slope, b1 is the same thing as the posttest difference between the means for the two groups. How can a slope be a difference between means? To see this, you have to take a look at a graph of what’s going on. In the graph, we show the posttest on the vertical axis. This is exactly the same as the two bell-shaped curves shown in the graphs above except that here they’re turned on their side. On the horizontal axis we plot the Z variable. This variable only has two values, a 0 if the person is in the control group or a 1 if the person is in the program group. We call this kind of variable a “dummy” variable because it is a “stand in” variable that represents the program or treatment conditions with its two values (note that the term “dummy” is not meant to be a slur against anyone, especially the people participating in your study). The two points in the graph indicate the average posttest value for the control ( Z = 0 ) and treated ( Z = 1 ) cases. The line that connects the two dots is only included for visual enhancement purposes – since there are no Z values between 0 and 1 there can be no values plotted where the line is. Nevertheless, we can meaningfully speak about the slope of this line, the line that would connect the posttest means for the two values of Z . Do you remember the definition of slope? (Here we go again, back to high school!). The slope is the change in y over the change in x (or, in this case, Z ). But we know that the “change in Z ” between the groups is always equal to 1 (i.e. 1 - 0 = 1). So, the slope of the line must be equal to the difference between the average y -values for the two groups. That’s what I set out to show (reread the first sentence of this paragraph). b1 is the same value that you would get if you just subtract the two means from each other (in this case, because we set the treatment group equal to 1, this means we are subtracting the control group out of the treatment group value. A positive value implies that the treatment group mean is higher than the control, a negative means it’s lower). But remember at the very beginning of this discussion I pointed out that just knowing the difference between the means was not good enough for estimating the treatment effect because it doesn’t take into account the variability or spread of the scores. So how do we do that here? Every regression analysis program will give, in addition to the beta values, a report on whether each beta value is statistically significant. They report a t -value that tests whether the beta value differs from zero. It turns out that the t -value for the b1 coefficient is the exact same number that you would get if you did a t-test for independent groups. And, it’s the same as the square root of the F value in the two group one-way ANOVA (because t2 = F).

Here’s a few conclusions from all this:

the t-test, one-way ANOVA and regression analysis all yield same results in this case
the regression analysis method utilizes a dummy variable ( Z ) for treatment
regression analysis is the most general model of the three.

Cookie Consent

Conjointly uses essential cookies to make our site work. We also use additional cookies in order to understand the usage of the site, gather audience analytics, and for remarketing purposes.

For more information on Conjointly's use of cookies, please read our Cookie Policy .

Which one are you?

I am new to conjointly, i am already using conjointly.

One-Group Posttest Only Design: An Introduction

The one-group posttest-only design (a.k.a. one-shot case study ) is a type of quasi-experiment in which the outcome of interest is measured only once after exposing a non-random group of participants to a certain intervention.

The objective is to evaluate the effect of that intervention which can be:

A training program
A policy change
A medical treatment, etc.

One-group posttest-only design representation

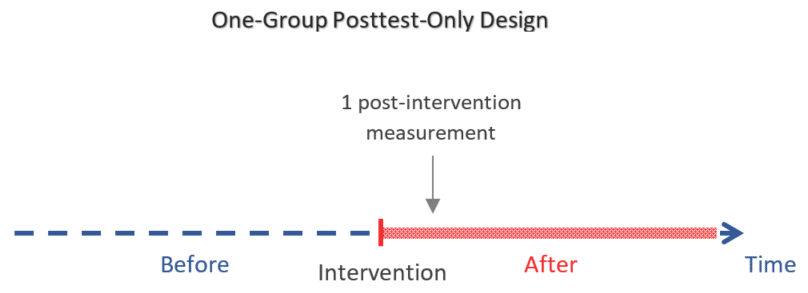
As in other quasi-experiments, the group of participants who receive the intervention is selected in a non-random way (for example according to their choosing or that of the researcher).

The one-group posttest-only design is especially characterized by having:

No control group
No measurements before the intervention

It is the simplest and weakest of the quasi-experimental designs in terms of level of evidence as the measured outcome cannot be compared to a measurement before the intervention nor to a control group.

So the outcome will be compared to what we assume will happen if the intervention was not implemented. This is generally based on expert knowledge and speculation.

Next we will discuss cases where this design can be useful and its limitations in the study of a causal relationship between the intervention and the outcome.

Advantages and Limitations of the one-group posttest-only design

Advantages of the one-group posttest-only design, 1. advantages related to the non-random selection of participants:.

Ethical considerations: Random selection of participants is considered unethical when the intervention is believed to be harmful (for example exposing people to smoking or dangerous chemicals) or on the contrary when it is believed to be so beneficial that it would be malevolent not to offer it to all participants (for example a groundbreaking treatment or medical operation).
Difficulty to adequately randomize subjects and locations: In some cases where the intervention acts on a group of people at a given location, it becomes infeasible to adequately randomize subjects (ex. an intervention that reduces pollution in a given area).

2. Advantages related to the simplicity of this design:

Feasible with fewer resources than most designs: The one-group posttest-only design is especially useful when the intervention must be quickly introduced and we do not have enough time to take pre-intervention measurements. Other designs may also require a larger sample size or a higher cost to account for the follow-up of a control group.
No temporality issue: Since the outcome is measured after the intervention, we can be certain that it occurred after it, which is important for inferring a causal relationship between the two.

Limitations of the one-group posttest-only design

1. selection bias:.

Because participants were not chosen at random, it is certainly possible that those who volunteered are not representative of the population of interest on which we intend to draw our conclusions.

2. Limitation due to maturation:

Because we don’t have a control group nor a pre-intervention measurement of the variable of interest, the post-intervention measurement will be compared to what we believe or assume would happen was there no intervention at all.

The problem is when the outcome of interest has a natural fluctuation pattern (maturation effect) that we don’t know about.

So since certain factors are essentially hard to predict and since 1 measurement is certainly not enough to understand the natural pattern of an outcome, therefore with the one-group posttest-only design, we can hardly infer any causal relationship between intervention and outcome.

3. Limitation due to history:

The idea here is that we may have a historical event, which may also influence the outcome, occurring at the same time as the intervention.

The problem is that this event can now be an alternative explanation of the observed outcome. The only way out of this is if the effect of this event on the outcome is well-known and documented in order to account for it in our data analysis.

This is why most of the time we prefer other designs that include a control group (made of people who were exposed to the historical event but not to the intervention) as it provides us with a reference to compare to.

Example of a study that used the one-group posttest-only design

In 2018, Tsai et al. designed an exercise program for older adults based on traditional Chinese medicine ideas, and wanted to test its feasibility, safety and helpfulness.

So they conducted a one-group posttest-only study as a pilot test with 31 older adult volunteers. Then they evaluated these participants (using open-ended questions) after receiving the intervention (the exercise program).

The study concluded that the program was safe, helpful and suitable for older adults.

What can we learn from this example?

1. work within the design limitations:.

Notice that the outcome measured was the feasibility of the program and not its health effects on older adults.

The purpose of the study was to design an exercise program based on the participants’ feedback. So a pilot one-group posttest-only study was enough to do so.

For studying the health effects of this program on older adults a randomized controlled trial will certainly be necessary.

2. Be careful with generalization when working with non-randomly selected participants:

For instance, participants who volunteered to be in this study were all physically active older adults who exercise regularly.

Therefore, the study results may not generalize to all the elderly population.

Shadish WR, Cook TD, Campbell DT. Experimental and Quasi-Experimental Designs for Generalized Causal Inference . 2nd Edition. Cengage Learning; 2001.
Campbell DT, Stanley J. Experimental and Quasi-Experimental Designs for Research . 1st Edition. Cengage Learning; 1963.

30 8.1 Experimental design: What is it and when should it be used?

Learning objectives.

Define experiment
Identify the core features of true experimental designs
Describe the difference between an experimental group and a control group
Identify and describe the various types of true experimental designs

Experiments are an excellent data collection strategy for social workers wishing to observe the effects of a clinical intervention or social welfare program. Understanding what experiments are and how they are conducted is useful for all social scientists, whether they actually plan to use this methodology or simply aim to understand findings from experimental studies. An experiment is a method of data collection designed to test hypotheses under controlled conditions. In social scientific research, the term experiment has a precise meaning and should not be used to describe all research methodologies.

Experiments have a long and important history in social science. Behaviorists such as John Watson, B. F. Skinner, Ivan Pavlov, and Albert Bandura used experimental design to demonstrate the various types of conditioning. Using strictly controlled environments, behaviorists were able to isolate a single stimulus as the cause of measurable differences in behavior or physiological responses. The foundations of social learning theory and behavior modification are found in experimental research projects. Moreover, behaviorist experiments brought psychology and social science away from the abstract world of Freudian analysis and towards empirical inquiry, grounded in real-world observations and objectively-defined variables. Experiments are used at all levels of social work inquiry, including agency-based experiments that test therapeutic interventions and policy experiments that test new programs.

Several kinds of experimental designs exist. In general, designs considered to be true experiments contain three basic key features:

random assignment of participants into experimental and control groups
a “treatment” (or intervention) provided to the experimental group
measurement of the effects of the treatment in a post-test administered to both groups

Some true experiments are more complex. Their designs can also include a pre-test and can have more than two groups, but these are the minimum requirements for a design to be a true experiment.

Experimental and control groups

In a true experiment, the effect of an intervention is tested by comparing two groups: one that is exposed to the intervention (the experimental group , also known as the treatment group) and another that does not receive the intervention (the control group ). Importantly, participants in a true experiment need to be randomly assigned to either the control or experimental groups. Random assignment uses a random number generator or some other random process to assign people into experimental and control groups. Random assignment is important in experimental research because it helps to ensure that the experimental group and control group are comparable and that any differences between the experimental and control groups are due to random chance. We will address more of the logic behind random assignment in the next section.

Treatment or intervention

In an experiment, the independent variable is receiving the intervention being tested—for example, a therapeutic technique, prevention program, or access to some service or support. It is less common in of social work research, but social science research may also have a stimulus, rather than an intervention as the independent variable. For example, an electric shock or a reading about death might be used as a stimulus to provoke a response.

In some cases, it may be immoral to withhold treatment completely from a control group within an experiment. If you recruited two groups of people with severe addiction and only provided treatment to one group, the other group would likely suffer. For these cases, researchers use a control group that receives “treatment as usual.” Experimenters must clearly define what treatment as usual means. For example, a standard treatment in substance abuse recovery is attending Alcoholics Anonymous or Narcotics Anonymous meetings. A substance abuse researcher conducting an experiment may use twelve-step programs in their control group and use their experimental intervention in the experimental group. The results would show whether the experimental intervention worked better than normal treatment, which is useful information.

The dependent variable is usually the intended effect the researcher wants the intervention to have. If the researcher is testing a new therapy for individuals with binge eating disorder, their dependent variable may be the number of binge eating episodes a participant reports. The researcher likely expects her intervention to decrease the number of binge eating episodes reported by participants. Thus, she must, at a minimum, measure the number of episodes that occur after the intervention, which is the post-test . In a classic experimental design, participants are also given a pretest to measure the dependent variable before the experimental treatment begins.

Types of experimental design

Let’s put these concepts in chronological order so we can better understand how an experiment runs from start to finish. Once you’ve collected your sample, you’ll need to randomly assign your participants to the experimental group and control group. In a common type of experimental design, you will then give both groups your pretest, which measures your dependent variable, to see what your participants are like before you start your intervention. Next, you will provide your intervention, or independent variable, to your experimental group, but not to your control group. Many interventions last a few weeks or months to complete, particularly therapeutic treatments. Finally, you will administer your post-test to both groups to observe any changes in your dependent variable. What we’ve just described is known as the classical experimental design and is the simplest type of true experimental design. All of the designs we review in this section are variations on this approach. Figure 8.1 visually represents these steps.

Steps in classic experimental design: Sampling to Assignment to Pretest to intervention to Posttest

An interesting example of experimental research can be found in Shannon K. McCoy and Brenda Major’s (2003) study of people’s perceptions of prejudice. In one portion of this multifaceted study, all participants were given a pretest to assess their levels of depression. No significant differences in depression were found between the experimental and control groups during the pretest. Participants in the experimental group were then asked to read an article suggesting that prejudice against their own racial group is severe and pervasive, while participants in the control group were asked to read an article suggesting that prejudice against a racial group other than their own is severe and pervasive. Clearly, these were not meant to be interventions or treatments to help depression, but were stimuli designed to elicit changes in people’s depression levels. Upon measuring depression scores during the post-test period, the researchers discovered that those who had received the experimental stimulus (the article citing prejudice against their same racial group) reported greater depression than those in the control group. This is just one of many examples of social scientific experimental research.

In addition to classic experimental design, there are two other ways of designing experiments that are considered to fall within the purview of “true” experiments (Babbie, 2010; Campbell & Stanley, 1963). The posttest-only control group design is almost the same as classic experimental design, except it does not use a pretest. Researchers who use posttest-only designs want to eliminate testing effects , in which participants’ scores on a measure change because they have already been exposed to it. If you took multiple SAT or ACT practice exams before you took the real one you sent to colleges, you’ve taken advantage of testing effects to get a better score. Considering the previous example on racism and depression, participants who are given a pretest about depression before being exposed to the stimulus would likely assume that the intervention is designed to address depression. That knowledge could cause them to answer differently on the post-test than they otherwise would. In theory, as long as the control and experimental groups have been determined randomly and are therefore comparable, no pretest is needed. However, most researchers prefer to use pretests in case randomization did not result in equivalent groups and to help assess change over time within both the experimental and control groups.

Researchers wishing to account for testing effects but also gather pretest data can use a Solomon four-group design. In the Solomon four-group design , the researcher uses four groups. Two groups are treated as they would be in a classic experiment—pretest, experimental group intervention, and post-test. The other two groups do not receive the pretest, though one receives the intervention. All groups are given the post-test. Table 8.1 illustrates the features of each of the four groups in the Solomon four-group design. By having one set of experimental and control groups that complete the pretest (Groups 1 and 2) and another set that does not complete the pretest (Groups 3 and 4), researchers using the Solomon four-group design can account for testing effects in their analysis.

Solomon four-group designs are challenging to implement in the real world because they are time- and resource-intensive. Researchers must recruit enough participants to create four groups and implement interventions in two of them.

Overall, true experimental designs are sometimes difficult to implement in a real-world practice environment. It may be impossible to withhold treatment from a control group or randomly assign participants in a study. In these cases, pre-experimental and quasi-experimental designs–which we will discuss in the next section–can be used. However, the differences in rigor from true experimental designs leave their conclusions more open to critique.

Experimental design in macro-level research

You can imagine that social work researchers may be limited in their ability to use random assignment when examining the effects of governmental policy on individuals. For example, it is unlikely that a researcher could randomly assign some states to implement decriminalization of recreational marijuana and some states not to in order to assess the effects of the policy change. There are, however, important examples of policy experiments that use random assignment, including the Oregon Medicaid experiment. In the Oregon Medicaid experiment, the wait list for Oregon was so long, state officials conducted a lottery to see who from the wait list would receive Medicaid (Baicker et al., 2013). Researchers used the lottery as a natural experiment that included random assignment. People selected to be a part of Medicaid were the experimental group and those on the wait list were in the control group. There are some practical complications macro-level experiments, just as with other experiments. For example, the ethical concern with using people on a wait list as a control group exists in macro-level research just as it does in micro-level research.

Key Takeaways

True experimental designs require random assignment.
Control groups do not receive an intervention, and experimental groups receive an intervention.
The basic components of a true experiment include a pretest, posttest, control group, and experimental group.
Testing effects may cause researchers to use variations on the classic experimental design.
Classic experimental design- uses random assignment, an experimental and control group, as well as pre- and posttesting
Control group- the group in an experiment that does not receive the intervention
Experiment- a method of data collection designed to test hypotheses under controlled conditions
Experimental group- the group in an experiment that receives the intervention
Posttest- a measurement taken after the intervention
Posttest-only control group design- a type of experimental design that uses random assignment, and an experimental and control group, but does not use a pretest
Pretest- a measurement taken prior to the intervention
Random assignment-using a random process to assign people into experimental and control groups
Solomon four-group design- uses random assignment, two experimental and two control groups, pretests for half of the groups, and posttests for all
Testing effects- when a participant’s scores on a measure change because they have already been exposed to it
True experiments- a group of experimental designs that contain independent and dependent variables, pretesting and post testing, and experimental and control groups

Image attributions

exam scientific experiment by mohamed_hassan CC-0

Foundations of Social Work Research Copyright © 2020 by Rebecca L. Mauldin is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.