heat capacity problem solving

Chemistry Steps

General Chemistry

Thermochemistry.

In the previous post , we talked about heat capacity, specific heat, and the formula for the relationship between these and the change in temperature.

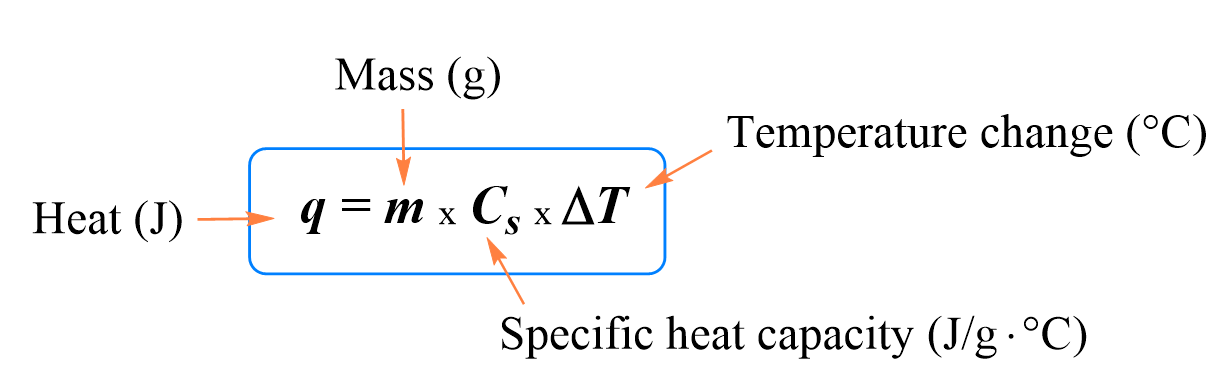
Below are some additional practice examples of heat capacity problems. 

When solving a problem related to heat capacity and heat transfer, remember that most of the time, it is assumed the heat is not lost, and it only flows from the object with a higher temperature to the colder one:

The second expression adding the lost and gained heat is easier to use because you do not need to remember which one has a negative sign.

How much heat does it take to increase the temperature of a 540.6-g sample of Fe from 20.0 °C to 84.3 °C? The specific heat of iron = 0.450 J/g °C.

Calculate the specific heat capacity of a metal if a 17.0 g sample requires 481 J to change the temperature of the metal from 25.0 °C to 67.0 °C?

Calculate the energy of combustion for one mole of butane if burning a 0.367 g sample of butane (C 4 H 10 ) has increased the temperature of a bomb calorimeter by 7.73 °C. The heat capacity of the bomb calorimeter is 2.36 kJ/ °C.

How many joules of energy is required to melt 40.0 g of ice at 0 °C? The heat of fusion (Δ H fus ) for ice is 334.0 J/g.

How many kJ of energy does it take to change 36.0 g of ice at -15.0 °C to water at 0. °C ? The specific heat of ice is 2.10 J/g°C and the heat of fusion (Δ H fus ) for ice is 334.0 J/g.

• Energy Related to Heat and Work
• Endothermic and Exothermic Processes
• Heat Capacity and Specific Heat
• What is Enthalpy
• Constant-Pressure Calorimetry
• Bomb calorimeter – Constant Volume Calorimetry
• Stoichiometry and Enthalpy of Chemical Reactions
• Hess’s Law and Enthalpy of Reaction
• Hess’s Law Practice Problems
• Standard Enthalpies of Formation
• Enthalpy of Reaction from Enthalpies of Formation
• Thermochemistry Practice Problems

Leave a Comment Cancel reply

Notify me of followup comments via e-mail. You can also subscribe without commenting.

• Exam Center
• Ticket Center
• Flash Cards
• Heat and Thermal Physics

Specific Heat Problems with Answers

Specific heat capacity is a fundamental concept in physics, describing the amount of heat energy, Q, required to raise the temperature of a unit mass (one kilogram or one gram) of a substance by one degree Celsius or Kelvin. 

This guide provides several practice problems with solutions to help the students grasp this concept.

Definition: 

If $m$ kilogram of a substance absorbs $Q$ joules of heat energy from a heat source and its temperature changes by $\Delta T=T_{final}-T_{initial}$, then its specific heat capacity is found by the following formula \[c=\frac{Q}{m\Delta T}\] This equation applies only when there is a temperature change.

Problems involving phase change are excluded from using this equation. Refer to the following pages for them:

Heat of fusion: formula and solved problems

Heat of vaporization: formula and solved problems

With this information in mind, we can now solve some specific heat problems to further understand its definition.

Specific Heat Problems

Problem (1): A chunk of steel with a mass of 1.57 kg absorbs a net thermal energy of $2.5\times 10^{5}$ J and increases its temperature by 355°C. What is the specific heat of the steel?

Solution : the specific heat of a substance is defined as the energy transferred ($Q$) to a system divided by the mass ($m$) of the system and the change in its temperature ($\Delta T$). Its formula is \[c\equiv \frac {Q}{m\Delta T}\]  Substituting the given numerical values into the above formula, we have \begin{align*} c&=\frac {Q}{m\Delta T}\\ \\ &=\frac{2.5\times 10^{5}}{(1.57)(273+355)}\\ \\&=4485.51\quad{\rm J/kg\cdot\,^{\circ}C}\end{align*} Where ${\rm J/kg\cdot\,^{\circ}C}$ is the SI unit of specific heat. 

Problem (2): One kilogram of water receives 4190 J of thermal energy, causing its temperature to increase by one degree Celsius. What is the specific heat capacity of water?

Solution: The specific heat capacity is the amount of heat energy required to raise the temperature of a system with a mass of $m$ by $\Delta T$ so applying its formula we get \begin{align*} c&=\frac {Q}{m\Delta T}\\ \\&=\frac{4190\,J}{(1\,kg)(1\,K)}\\ \\&=4190 \quad{\rm J/kg\cdot K}\end{align*}

Problem (3):  m kilogram of ice is heated, and its temperature increases from -10°C to -5°C. A larger amount of energy is added to the same mass of water, and the change in its temperature is from 15°C to 20°C. From these observations, compare the specific heat capacities of ice and water.

Solution : The heats added to the ice and water are $Q_i=m_ic_i \Delta T_i$ and $Q_w=m_wc_w \Delta T_w$, respectively. Now, solving for mass m and equating them (since it is said in the question that the mass of both samples is the same), we can get \begin{align*} m_i &= m_w\\\frac{Q_i}{c_i\Delta T_i}&=\frac{Q_w}{c_w \Delta T_w}\\ \\ \Rightarrow \frac{c_i}{c_w} &= \Big(\frac{Q_i}{Q_w}\Big)\Big(\frac{\Delta T_w}{\Delta T_i}\Big)\\ \\ &=\Big(\frac{Q_i}{Q_w}\Big) \Big(\frac{20-15}{-5-(-10)}\Big)\\ \\&=\Big(\frac{Q_i}{Q_w}\Big)\end{align*}Since $Q_i < Q_w$, we conclude that the specific heat capacity of ice is less than that of water.

A look at the specific heat table can confirm this. $c_i= 2090\,{\rm J/kg.K}$ and $c_w=4190\,{\rm J/kg.K}$. 

Problem (4): The temperature of a sample of iron with a mass of 10.0 g changed from 50.4°C to 25.0°C with the release of 47 calories of heat. What is the specific heat of iron? 

Solution : Initial and final temperatures are $T_i=50.4^\circ$ and $T_f=25^\circ$, respectively. Applying the specific heat equation and substituting the numerical values, we get \begin{align*} c&=\frac{Q}{m\Delta T}\\ \\&=\frac{47\, {\rm cal}}{1\,{\rm g}(50.4-25)}\\ \\ &=1.850\quad {\rm cal/g\cdot K}\end{align*}

Problem (5): the temperature of a 200-g sample of an unknown substance changed from 40°C to 25°C. In the process, the substance released 569 calories of energy. What is the specific heat capacity of the substance? 

Solution : again applying the specific heat definition, we have \begin{align*} c&=\frac{Q}{m\Delta T}\\ \\ &=\frac{-569\, {\rm cal}}{200\,{\rm g}\,(25-40)}\\ \\&=0.19 \quad {\rm cal/g\cdot K}\end{align*} since thermal energy has left the substance so a negative sign is placed.  

Problem (6): A 200-g sample of an unknown object is heated using 100 J such that its temperature rises by 2°C. What is the specific heat of this unknown object?

Solution : in this problem, the transferred heat $Q$ and the change in temperature $\Delta T$ are given. Using specific heat capacity formula we have  \begin{align*} c&=\frac{Q}{m\Delta T}\\ \\ &=\frac{100\, {\rm J}}{0.2\,{\rm kg}\,(2\,^\circ {\rm C})}\\ \\&=500 \quad {\rm J/kg\cdot ^\circ C}\end{align*}

Problem (7): What is the specific heat of metal if its mass is 27 g and it requires 420 J of heat energy to increase its temperature from 25°C to 50°C? 

Solution : applying the specific heat formula, we get \begin{align*} c&=\frac{Q}{m\Delta T}\\ \\&=\frac{420\,{\rm J}}{0.27\,{\rm kg}\times (50-25)}\\ \\&=62.2\quad {\rm \frac{J}{kg\cdot\,^\circ C}}\end{align*} Be sure to convert grams to kilograms. 

In another type of problem, the specific heat capacity is determined by calorimetry.

In calorimetry problems, the specific heat of a sample is determined by inserting it into a certain amount of water with a known temperature. 

This system is isolated so the sum of all energy gains or losses by all objects in the system is zero i.e. $\Sigma Q_i=0$ where $Q_i$ is the energy of the ith object.

If we measure the temperature of the equilibrium point, then we can solve the equation above for the unknown specific heat to find it. 

Below, some problems for finding the heat capacity using this method are presented.

Problem (8): A 125-g block of a substance with unknown specific heat at a temperature of 90°C is placed in an isolated box containing 0.326 kg of water at 20°C. The equilibrium temperature of the system is 22.4°C. What is the block's specific heat?

Solution : since the temperature of the block is higher than the water the block loses thermal energy and water gains it. Equate these, $Q_{gain}=-Q_{lose}$, and solve for the unknown specific heat. \begin{align*} m_w c_w (T-T_w) &= -m_x c_x (T-T_x)\\ \\ \Rightarrow c_x&=\frac{m_w c_w (T-T_w)}{m_x (T_x-T)}\\ \\ &=\frac{(0.326)(4190)(22.4-20)}{(0.125)(90-22.4)}\\ \\&=388\quad {\rm J/kg\cdot\, ^\circ C}\end{align*} In calorimetry problems, thermal energy is transferred from the warmer substance to the cooler object. 

Therefore, a negative is placed in front of the warmer object to ensure that both sides of the above equality become positive. 

For more practice about this, check out the page on  thermodynamics problems and solutions .

Problem (9): A piece of metal of unknown specific heat, weighing 25 g and temperature 90°C, is dropped into 150 g of water at 10°C. They finally reach thermal equilibrium at a temperature of 24°C. Calculate the unknown specific heat capacity. (Specific heat of water is 1.0 cal/g°C)

Solution : Since the equilibrium temperature $T_f$ is lower than the metal one, it loses as much heat as $Q_m=-m_m c_m (T_f-T_m)$ and the water gains heat as much as $Q_w=m_w c_w (T_f-T_w)$. 

As a rule of thumb keep in mind that, once any object loses heat we should place a negative in front of it. 

Conservation of energy says that $Q_w=Q_m$, therefore we have \begin{align*} m_w c_w (T_f-T_w)&= -m_m c_m (T_f-T_m) \\ \\ \Rightarrow c_m &= \frac{m_w c_w (T_f-T_w)}{m_m \,(T_m-T_f)}\\ \\ &=\frac{(150)(1)(24-10)}{25\times(90-24)}\\ \\&=1.27\quad {\rm cal/g\cdot\,^\circ C}\end{align*}

Problem (10):  a piece of unknown substance with a mass of 2 kg and a temperature of 280 Kelvins is brought in thermally contact with a 5-kg block of copper initially at 320 K.

This system is in isolation. After the system reaches thermal equilibrium, its temperature becomes 290 K.

What is the specific heat of the unknown substance in cal/g.°C? (Specific heat of the copper is 0.093 cal/g.°C).

Solution : copper loses heat and the unknown substance gains that amount of lost heat, by considering complete isolation. As previous questions, we get \begin{align*} m_s c_s (T_f-T_s)&= -m_c c_c (T_f-T_c) \\ \\ \Rightarrow c_s &= \frac{m_c c_c (T_c-T_f)}{m_s \,(T_f-T_s)}\\ \\&=\frac{(5000)(0.093)(320-290)}{2000\times(290-280)}\\ \\ &=0.6975 \quad {\rm cal/g\cdot K}\end{align*} In above, the subscripts $s$ and $c$ denote the substance and copper, respectively. 

Note : in calorimetry equations where a temperature change appears, it's possible to use either Celsius or Kelvin temperatures because a change in Celsius equals a change in Kelvin. 

Problem (11): a 20-g block of a solid initially at 70°C is placed in 100 g of a fluid with a temperature of 20°C. After a while, the system reaches thermal equilibrium at a temperature of 30°C. What is the ratio of the specific heat of the solid to that of the fluid? 

Solution : solid loses heat and fluid absorbs it so $Q_f=-Q_s$ where f and s denote the fluid and solid, respectively. From the definition of specific heat, we can find the heat transferred during a process as below \begin{align*} m_f c_f (T-T_f) &= -m_s c_s (T-T_s)\\ \\ \Rightarrow \frac{c_f}{c_s} &=\frac{m_s (T_s-T)}{m_f (T-T_f)}\\ \\ &= \frac{(20)(70-30)}{(100)(30-20)}\\ \\ &=0.8\end{align*} Therefore, the specific heat capacity of fluid is less than that of solid. 

Problem (12): A chunk of metal with a mass of 245.7 g at 75.2°C is placed in 115.43 g of water initially at a temperature of 22.6°C. The metal and water reach the final equilibrium temperature of 34.6°C. If no heat is exchanged between the system and its surroundings, what is the specific heat of the metal? (specific heat of water is 1 cal/g °C). 

Solution : Since no heat is lost to the surroundings, by conservation of energy we have $Q_{water}=-Q_{metal}$ \begin{align*}Q_{water}&=-Q_{metal}\\ \\m_w c_w (T_f-T_w) &=-m_{metal} \, c_{metal} (T_f-T_{metal})\\ &\\ \Rightarrow c_{metal}&=\frac{m_w c_w (T_f-T_w)}{m_{metal}(T_{metal}-T_f)}\\&\\ &=\frac{(115.43)(1)(34.6-22.6)}{(245.7)(75.2-34.6)}\\ \\&=0.13 \quad {\rm cal/g\cdot^\circ C}\end{align*} where $T_f$ is the equilibrium temperature. 

Now, we solve some problems with specific heat capacity using calorimetry. 

Problem (13) :  how many liters of water at 80°C should be mixed with 40 liters of water at 10°C to have a mixture with a final temperature of 40°C?

Solution : conservation of energy tells us that $\Sigma Q=0$ that is $Q_{lost}+Q_{gain}=0$. By considering no heat exchange with the environment, hotter objects lose heat and colder ones gain it. Thus, the amount of heat lost by 80°C - water is \begin{align*} Q_{lost}&=mc(T_f-T_i)\\&=mc(40-80)\\&=-40mc\end{align*} and also the heat gained by 40°C - water is \begin{align*} Q_{gain}&=m'c(T_f-T_i)\\&=40\times c\times (40-10)\\&=1200c\end{align*}Therefore, by equating those two heats, we get the unknown mass of the water \begin{align*} Q_{gain}&=-Q_{lost}\\1200c&=-(-40mc)\\1200&=40m \Rightarrow m&=30,{\rm Lit}\end{align*}

Problem (14):   200 g of water at 22.5°C is mixed with 150 grams of water at 40°C, after reaching the thermal equilibrium, what is the final temperature of the water? 

Solution : using the principle of conservation of energy, we have $Q_{lost}+Q_{gain}=0$. Substituting the specific heat equation into it, we get \begin{gather*} m_1 c_w (T_f-T_1)+m_2 c_w (T_f-T_2)=0\\ \\ 200 (T_f-22.5)+150 (T_f-40)=0\\ \\ \Rightarrow 350T_f=10500 \\ \\ \Rightarrow T_f= 30^{\circ}C \end{gather*} where $T_f$ is the equilibrium (final) temperature of the mixture. Also, the specific heat capacity of the water is dropped from both sides.

Problem (15): In a container, 1000 g of water and 200 g of ice are in thermal equilibrium. A piece of metal with a specific heat capacity of $c_m=400\,{\rm J/kg.K}$ and a temperature of 250°C is dropped into the mixture.  How much should the minimum mass of the metal be to melt down all of the ice? (heat of fusion of ice is $L_f=336\,{\rm \frac{kJ}{kg}}$.

Solution : minimum mass means that the metal has enough heat energy to melt down the ice completely and not raise the temperature of the system. Thus, the amount of heat energy released by $m$ gram of the metal to reach from 250°C to 0°C is $Q_{lost}=mc(T_f-T_i)$ where $T_f$ is the equilibrium temperature which is 0°C.

On the other hand, the required energy for melting 200 g of ice is also obtained as below \[Q_{gain}=m_{ice} L_f=200\times 336\times 10^{3}\,{\rm \frac{J}{kg}}\] where $L_f$ is the latent heat of the ice. Now, conservation of energy tells us that equate them and find the unknown metal's mass \begin{gather*}m_{metal}\,c(T_f-T_i)+m_{ice}L_f=0 \\ \\ m_{metal} \times 400\times (0-250)+200\times 336 \times 10^{3}=0 \\ \\  \Rightarrow m_{metal}=672 \quad {\rm g} \end{gather*} If the metal's mass is greater than this value, the excess heat will cause the final temperature of the system goes higher. 

For more exercise, you can also practice these heat problems . 

In the end, we provided some specific heat capacities at room temperature. 

Author : Dr. Ali Nemati Last Update: 1/9/2021

© 2015 All rights reserved. by Physexams.com

• Science Notes Posts
• Contact Science Notes
• Todd Helmenstine Biography
• Anne Helmenstine Biography
• Free Printable Periodic Tables (PDF and PNG)
• Periodic Table Wallpapers
• Interactive Periodic Table
• Periodic Table Posters
• Science Experiments for Kids
• How to Grow Crystals
• Chemistry Projects
• Fire and Flames Projects
• Holiday Science
• Chemistry Problems With Answers
• Physics Problems
• Unit Conversion Example Problems
• Chemistry Worksheets
• Biology Worksheets
• Periodic Table Worksheets
• Physical Science Worksheets
• Science Lab Worksheets
• My Amazon Books

Specific Heat Example Problem

Specific heat is the amount of heat per unit mass needed to increase the temperature of a material by one degree Celsius or Kelvin. These three specific heat example problems will show how to find the specific heat of a material or other information involving the specific heat.

Specific Heat Equation

The equation most commonly associated with specific heat is

where Q = Heat energy m = mass c = specific heat ΔT = change in temperature = (T final – T initial )

A good way to remember this formula is Q = “em cat”

Basically, this equation is used to determine the amount of heat added to a material to raise the temperature some amount (or the amount lost as the material cools).

This equation only applies to materials that stay in the same state of matter (solid, liquid, or gas) as the temperature changes. Phase changes require additional energy considerations.

Specific Heat Example Problem – Find the Amount of Heat

Question : A 500 gram cube of lead is heated from 25 °C to 75 °C. How much energy was required to heat the lead? The specific heat of lead is 0.129 J/g°C.

Solution : First, let’s the variables we know.

m = 500 grams c = 0.129 J/g°C ΔT = (T final – T initial ) = (75 °C – 25 °C) = 50 °C

Plug these values into the specific heat equation from above.

Q = mcΔT

Q = (500 grams)·(0.129 J/g°C)·(50 °C)

Answer : It took 3225 Joules of energy to heat the lead cube from 25 °C to 75 °C.

Specific Heat Example Problem – Find the Specific Heat

Question: A 25-gram metal ball is heated 200 °C with 2330 Joules of energy. What is the specific heat of the metal?

Solution : List the information we know.

m = 25 grams ΔT = 200 °C Q = 2330 J

Place these into the specific heat equation.

2330 J = (25 g)c(200 °C)

2330 J = (5000 g°C)c

Divide both sides by 5000 g°C

c = 0.466 J/g°C

Answer : The specific heat of the metal is 0.466 J/g°C.

Specific Heat Example Problem – Find the Initial Temperature

Question: A hot 1 kg chunk of copper is allowed to cool to 100°C. If the copper gave off 231 kJ of energy, what was the initial temperature of the copper? The specific heat of copper is 0.385 J/g°C.

Solution : List our given variables:

m = 1 kg T final = 100 °C Q = -231 kJ (The negative sign is because the copper is cooling and losing energy.) c = 0.385 J/g°C

We need to make our units consistent with the specific heat units, so let’s convert the mass and energy units.

m = 1 kg = 1000 grams

1 kJ = 1000 J Q = -231 kJ · (1000 J/kJ) = -231000 J

Plug these values into the specific heat formula.

-231000 J = 1000 g · (0.385 J/g°C) · ΔT

-231000 J = 385 J/°C · ΔT

ΔT = -600 °C

ΔT = (T final – T initial )

Plug in the values for ΔT and T final .

-600 °C = (100 °C – T initial )

Subtract 100 °C from both sides of the equation.

-600 °C – 100 °C =  – T initial

-700 °C = – T initial

T initial  = 700 °C

Answer : The initial temperature of the copper chunk was 700 °C.

Related Posts

PhysicsTeacher.in

High School Physics + more

Numerical problems on Specific Heat Capacity with solutions

In this post, we will solve a few interesting numerical problems based on specific heat capacity. Learn more about Specific heat capacity here .

Solving numerical problems using specific heat capacity formula

Question 1] A tank holding 30 kg of water is heated by a 3 kW electric immersion heater. If the specific heat capacity of water is 4200 J/(kg ºC), estimate the time for the temperature to rise from 10 ºC to 60 ºC.

A 3 kW (3000 W) heater supplies 3000 J of heat energy per second. Let t = time taken in seconds to raise the temperature of the water by (60−10) = 50 ºC, ∴ heat supplied to water in time t seconds = (3000 × t) J …………. (1)

From the heat equation, we can say heat received by water =mass x specific heat capacity x temperature rise = 30 kg × 4200 J/(kg ºC) × 50 ºC = 30 x 4200 x 50 J…………….. (2)

Assuming heat supplied = heat received,

Hence, from equations 1 & 2 we get: 3000 × t = (30 × 4200 × 50)

t = (30 × 4200 × 50) / 3000 = 2100 seconds = 35 minutes

So the time estimate is 35 minutes. (answer)

Question 2 ]

A piece of aluminium of mass 0.5 kg is heated to 100 ºC and then placed in 0.4 kg of water at 10 ºC. If the resulting temperature of the mixture is 30 ºC, what is the specific heat capacity of aluminium if that of water is 4200 J/(kg ºC)?

When two substances at different temperatures are mixed, heat flows from the one at the higher temperature to the one at the lower temperature until both are at the same temperature i.e., the temperature of the mixture.

If there is no loss of heat, then in this case: Heat given out by aluminium = Heat taken in by water Using the heat equation and letting c be the specific heat capacity of aluminium in J/(kg ºC), we have

heat given out = 0.5 kg × c × (100 − 30) ºC heat taken in = 0.4 kg × 4200 J/(kg ºC) × (30 − 10) ºC

∴ 0.5 kg × c × 70 ºC = 0.4 kg × 4200 J/(kg ºC) × 20 ºC

35 c = 8 x 4200

c = ( 8 x 4200)/35 J/(kg ºC) = 960 J/(kg ºC)

Hence, the specific heat capacity of aluminium 960 J/(kg º

Related Posts:

• A piece of iron of mass 2.0 kg has a heat capacity of 966 J K-1. Find (i)…
• Calculate the heat capacity of a copper vessel of mass 150 g if the…
• 1300 J of heat energy is supplied to raise the temperature of 0.5 kg of…
• Calculate the amount of heat energy required to raise the temperature of…
• Find the time taken by a 500 W  heater to raise the temperature of 50 kg…
• A mass of 50 g of a certain metal at 150° C is immersed in 100 g of water…

• Science, Tech, Math ›
• Chemistry ›

Specific Heat Example Problem

Calculating the specific heat of a given substance

• Chemical Laws
• Periodic Table
• Projects & Experiments
• Scientific Method
• Biochemistry
• Physical Chemistry
• Medical Chemistry
• Chemistry In Everyday Life
• Famous Chemists
• Activities for Kids
• Abbreviations & Acronyms
• Weather & Climate
• Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
• B.A., Physics and Mathematics, Hastings College

This worked example problem demonstrates how to calculate the specific heat of a substance when given the amount of energy used to change the substance's temperature.

Specific Heat Equation and Definition

First, let's review what specific heat is and the equation you'll use to find it. Specific heat is defined as the amount of heat per unit mass needed to increase the temperature by one degree Celsius (or by 1 Kelvin). Usually, the lowercase letter "c" is used to denote specific heat. The equation is written:

Q = mcΔT (you can remember this by thinking "em-cat")

where Q is the heat that is added, c is specific heat, m is mass, and ΔT is the change in temperature. The usual units used for quantities in this equation are degrees Celsius for temperature (sometimes Kelvin), grams for mass, and specific heat reported in calorie/gram °C, joule/gram °C, or joule/gram K. You can also think of specific heat as heat capacity per mass basis of a material.

There are published tables of molar specific heats of many materials. Note that the specific heat equation does not apply for phase changes. This is because the temperature does not change. When working a problem, you'll either be given the specific heat values and asked to find one of the other values, or else asked to find specific heat.

Specific Heat Problem

It takes 487.5 J to heat 25 grams of copper from 25 °C to 75 °C. What is the specific heat in Joules/g·°C? Solution: Use the formula q = mcΔT where q = heat energy m = mass c = specific heat ΔT = change in temperature Putting the numbers into the equation yields:

487.5 J = (25 g)c(75 °C - 25 °C) 487.5 J = (25 g)c(50 °C) Solve for c: c = 487.5 J/(25g)(50 °C) c = 0.39 J/g·°C

Answer: The specific heat of copper is 0.39 J/g·°C.

• Heat of Formation Worked Problem
• Heat Capacity Example Problem
• Calorimetry and Heat Flow: Worked Chemistry Problems
• Calculate Energy Required to Turn Ice Into Steam
• Heat of Vaporization Example Problem
• Calculating the Final Temperature of a Reaction From Specific Heat
• Specific Heat Definition
• Heat of Fusion Example Problem: Melting Ice
• Specific Heat Capacity in Chemistry
• Calculate the Change in Entropy From Heat of Reaction
• Converting Kilometers to Meters
• Calculate Osmotic Pressure Example Problem
• A List of Common General Chemistry Problems
• Freezing Point Depression Example Problem
• Enthalpy Change Example Problem
• Introduction To Stoichiometry