double slit experiment notes

• IIT JEE Study Material
• Youngs Double Slit Experiment

Young's Double Slit Experiment

What is young’s double slit experiment.

Young’s double slit experiment uses two coherent sources of light placed at a small distance apart. Usually, only a few orders of magnitude greater than the wavelength of light are used. Young’s double slit experiment helped in understanding the wave theory of light , which is explained with the help of a diagram. As shown, a screen or photodetector is placed at a large distance, ‘D’, away from the slits.

Download Complete Chapter Notes of Wave Optics Download Now

JEE Main 2021 LIVE Physics Paper Solutions 24 Feb Shift-1 Memory-based

The original Young’s double slit experiment used diffracted light from a single source passed into two more slits to be used as coherent sources. Lasers are commonly used as coherent sources in modern-day experiments.

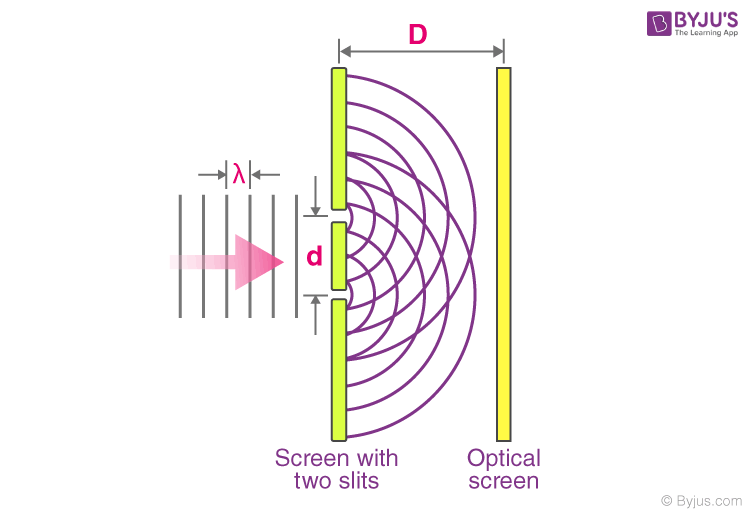
Table of Contents

• Position of Fringes
• Shape of Fringes
• Intensity of Fringes

Special Cases

• Displacement of Fringes

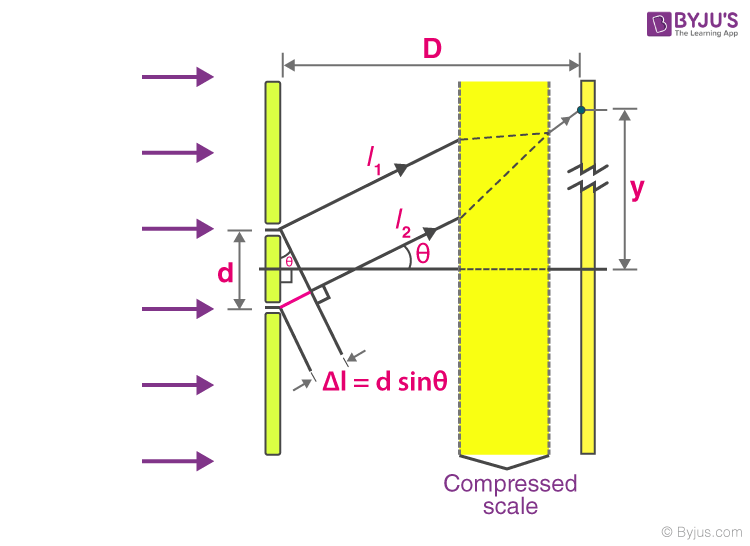
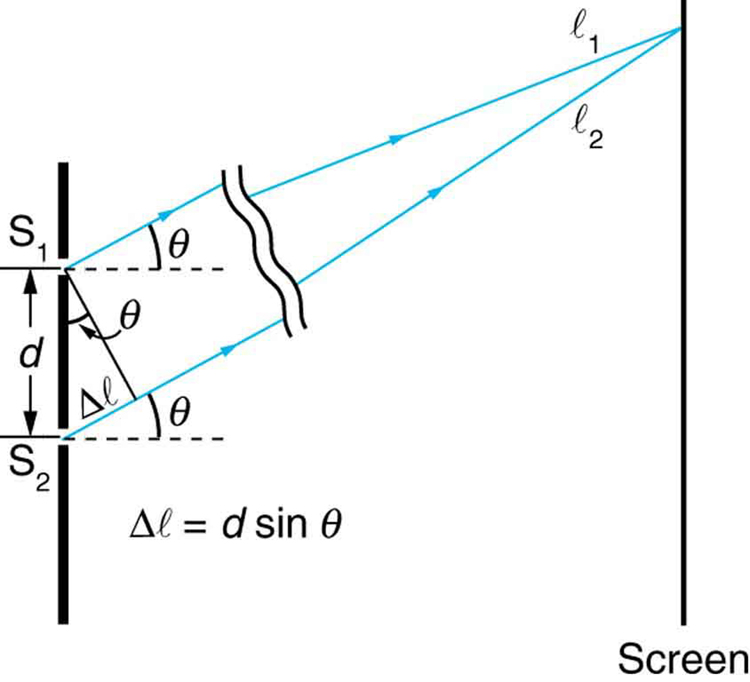
Each source can be considered a source of coherent light waves . At any point on the screen at a distance ‘y’ from the centre, the waves travel distances  l 1  and  l 2 to create a path difference of Δl at the point. The point approximately subtends an angle of θ at the sources (since the distance D is large, there is only a very small difference between the angles subtended at sources).

Derivation of Young’s Double Slit Experiment

Consider a monochromatic light source ‘S’ kept at a considerable distance from two slits: s 1 and s 2 . S is equidistant from s 1 and s 2 . s 1 and s 2 behave as two coherent sources as both are derived from S.

The light passes through these slits and falls on a screen which is at a distance ‘D’ from the position of slits s 1 and s 2 . ‘d’ is the separation between two slits.

If s 1 is open and s 2 is closed, the screen opposite to s 1 is closed, and only the screen opposite to s 2 is illuminated. The interference patterns appear only when both slits s 1 and s 2 are open.

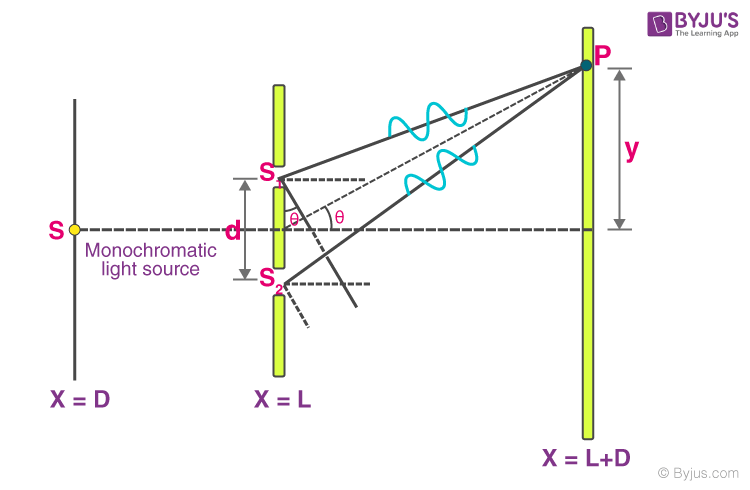
When the slit separation (d) and the screen distance (D) are kept unchanged, to reach P, the light waves from s 1 and s 2 must travel different distances. It implies that there is a path difference in Young’s double slit experiment between the two light waves from s 1 and s 2 .

Approximations in Young’s double slit experiment 

• Approximation  1: D > > d: Since D > > d, the two light rays are assumed to be parallel.
• Approximation  2:   d/λ >> 1:  Often, d is a fraction of a millimetre, and λ is a fraction of a micrometre for visible light.

Under these conditions, θ is small. Thus, we can use the approximation sin θ = tan θ ≈ θ = λ/d.

∴ path difference, Δz = λ/d

This is the path difference between two waves meeting at a point on the screen. Due to this path difference in Young’s double slit experiment, some points on the screen are bright, and some points are dark.

Now, we will discuss the position of these light and dark fringes and fringe width.

Position of Fringes in Young’s Double Slit Experiment

Position of bright fringes.

For maximum intensity or bright fringe to be formed at P,

Path difference, Δz = nλ (n = 0, ±1, ±2, . . . .)

i.e., xd/D = nλ

The distance of the n th   bright fringe from the centre is

x n = nλD/d

Similarly, the distance of the (n-1) th  bright fringe from the centre is

x (n-1) = (n -1)λD/d

Fringe width,  β =  x n   – x (n-1)  = nλD/d – (n -1)λD/d = λD/d

(n = 0, ±1, ±2, . . . .)

Position of Dark Fringes

For minimum intensity or dark fringe to be formed at P,

Path difference, Δz = (2n + 1) (λ/2) (n = 0, ±1, ±2, . . . .)

i.e., x = (2n +1)λD/2d

The distance of the n th   dark fringe from the centre is

x n = (2n+1)λD/2d

x (n-1) = (2(n-1) +1)λD/2d

Fringe width, β = x n   – x (n-1)  = (2n + 1) λD/2d – (2(n -1) + 1)λD/2d = λD/d

Fringe Width

The distance between two adjacent bright (or dark) fringes is called the fringe width.

If the apparatus of Young’s double slit experiment is immersed in a liquid of refractive index  (μ), then the wavelength of light and fringe width decreases ‘μ’ times.

If white light is used in place of monochromatic light, then coloured fringes are obtained on the screen, with red fringes larger in size than violet.

Angular Width of Fringes

Let the angular position of n th bright fringe is θ n, and because of its small value, tan θ n   ≈ θ n

Similarly, the angular position of (n+1) th bright fringe is θ n+1,  then

∴ The angular width of a fringe in Young’s double slit experiment is given by,

Angular width is independent of ‘n’, i.e., the angular width of all fringes is the same.

Maximum Order of Interference Fringes

But ‘n’ values cannot take infinitely large values as it would violate the 2 nd approximation.

i.e., θ is small (or) y < < D

When the ‘n’ value becomes comparable to d/ λ, path difference can no longer be given by d γ/D.

Hence for maxima, path difference = nλ

The above represents the box function or greatest integer function.

Similarly, the highest order of interference minima

The Shape of Interference Fringes in YDSE

From the given YDSE diagram, the path difference between the two slits is given by

The above equation represents a hyperbola with its two foci as, s 1 and s 2 .

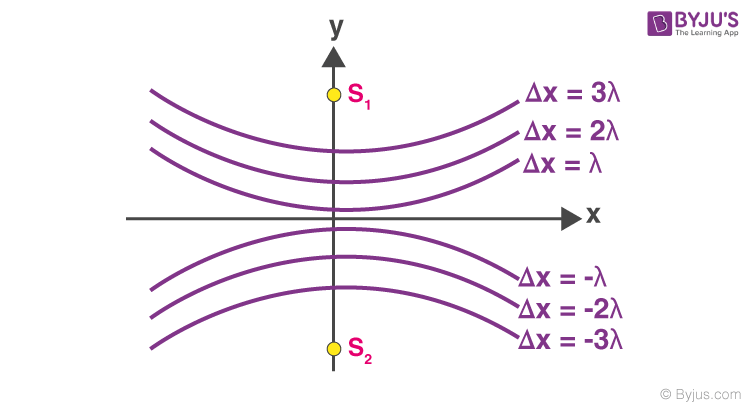
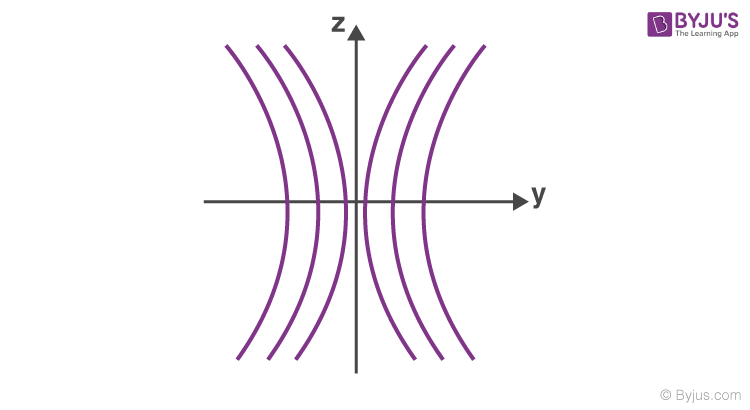
The interference pattern we get on the screen is a section of a hyperbola when we revolve the hyperbola about the axis s 1 s 2 .

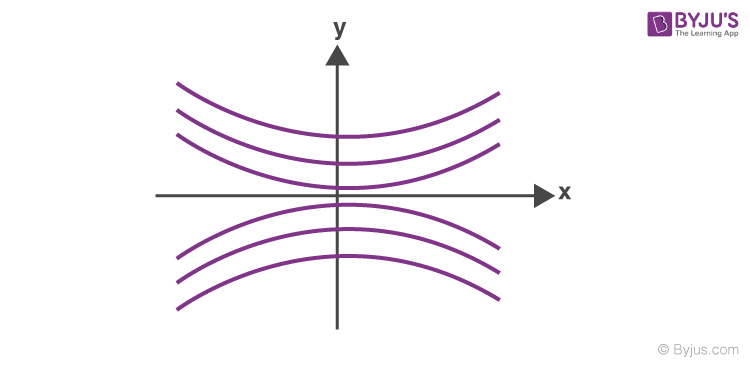
If the screen is a yz plane, fringes are hyperbolic with a straight central section.

If the screen is xy plane , the fringes are hyperbolic with a straight central section.

The Intensity of Fringes in Young’s Double Slit Experiment

For two coherent sources, s 1 and s 2 , the resultant intensity at point p is given by

I = I 1 + I 2 + 2 √(I 1 . I 2 ) cos φ

Putting I 1 = I 2 = I 0  (Since, d<<<D)

I = I 0 + I 0 + 2 √(I 0 .I 0 ) cos φ

I = 2I 0 + 2 (I 0 ) cos φ

I = 2I 0 (1 +  cos φ)

For maximum intensity

phase difference   φ = 2nπ

Then, path difference \(\begin{array}{l}\Delta x=\frac{\lambda }{{2}{\pi }}\left( {2}n{\pi } \right)\end{array} \) = nλ

The intensity of bright points is maximum and given by

I max = 4I 0

For minimum intensity

φ = (2n – 1) π

Phase difference φ = (2n – 1)π

Thus, the intensity of minima is given by

If I 1 ≠ I 2 , I min ≠ 0.

Rays Not Parallel to Principal Axis:

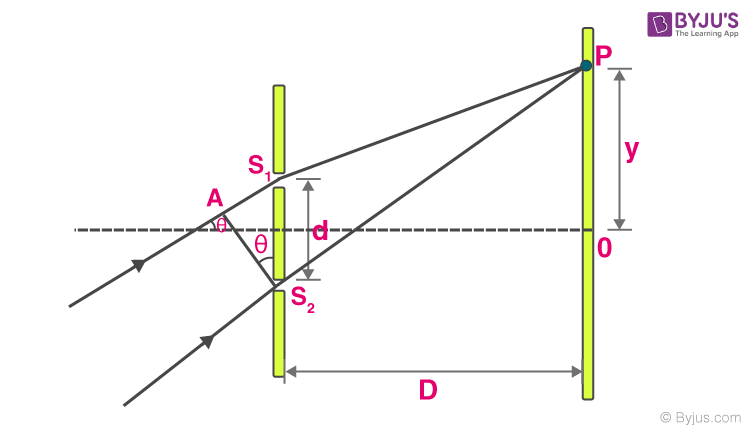
From the above diagram,

Using this, we can calculate different positions of maxima and minima.

Source Placed beyond the Central Line:

If the source is placed a little above or below this centre line, the wave interaction with S 1 and S 2 has a path difference at point P on the screen.

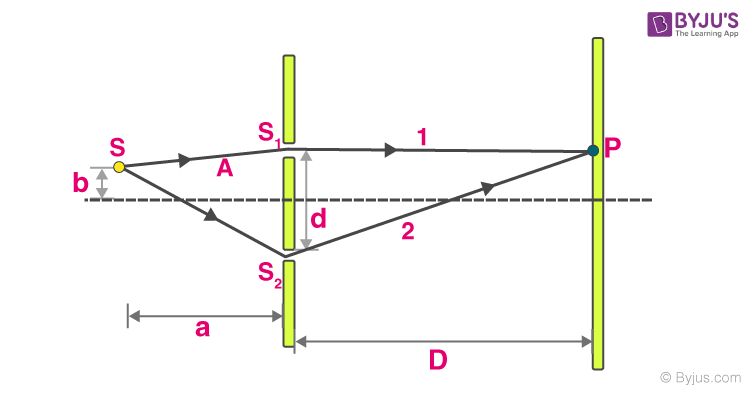
Δ x= (distance of ray 2) – (distance of ray 1)

= bd/a + yd/D → (*)

We know Δx = nλ for maximum

Δx = (2n – 1) λ/2 for minimum

By knowing the value of Δx from (*), we can calculate different positions of maxima and minima .

Displacement of Fringes in YDSE

When a thin transparent plate of thickness ‘t’ is introduced in front of one of the slits in Young’s double slit experiment, the fringe pattern shifts toward the side where the plate is present.

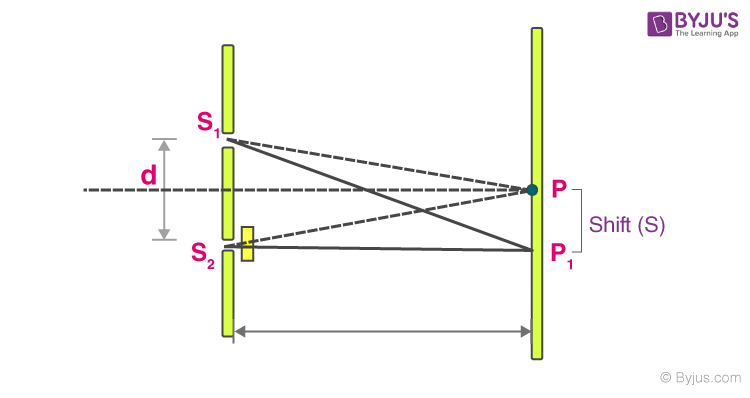
The dotted lines denote the path of the light before introducing the transparent plate. The solid lines denote the path of the light after introducing a transparent plate.

Where μt is the optical path.

Then, we get,

Term (1) defines the position of a bright or dark fringe; term (2) defines the shift that occurred in the particular fringe due to the introduction of a transparent plate.

Constructive and Destructive Interference

For constructive interference, the path difference must be an integral multiple of the wavelength.

Thus, for a bright fringe to be at ‘y’,

Or, y = nλD/d

Where n = ±0,1,2,3…..

The 0th fringe represents the central bright fringe.

Similarly, the expression for a dark fringe in Young’s double slit experiment can be found by setting the path difference as

Δl = (2n+1)λ/2

This simplifies to

(2n+1)λ/2 = y d/D

y = (2n+1)λD/2d

Young’s double slit experiment was a watershed moment in scientific history because it firmly established that light behaved like a wave.

The double slit experiment was later conducted using electrons , and to everyone’s surprise, the pattern generated was similar as expected with light. This would forever change our understanding of matter and particles, forcing us to accept that matter, like light, also behaves like a wave.

Wave Optics

Young’s double slit experiment.

Frequently Asked Questions on Young’s Double Slit Experiment

What was the concept explained by young’s double slit experiment.

Young’s double slit experiment helps in understanding the wave theory of light.

What are the formulas derived from Young’s double slit experiment?

For constructive interference, dsinθ = mλ , for m = 0,1,-1,2,-2

For destructive interference, dsinθ = (m+½)λ, for m = 0,1,-1,2,-2 Here, d is the distance between the slits. λ is the wavelength of the light waves.

What is called a fringe width?

The distance between consecutive bright or dark fringe is called the fringe width.

What kind of source is used in Young’s double slit experiment?

A coherent source is used in Young’s double slit experiment.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all JEE related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

Register with Aakash BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Wave Optics

Young’s double slit experiment, learning objectives.

By the end of this section, you will be able to:

• Explain the phenomena of interference.
• Define constructive interference for a double slit and destructive interference for a double slit.

Although Christiaan Huygens thought that light was a wave, Isaac Newton did not. Newton felt that there were other explanations for color, and for the interference and diffraction effects that were observable at the time. Owing to Newton’s tremendous stature, his view generally prevailed. The fact that Huygens’s principle worked was not considered evidence that was direct enough to prove that light is a wave. The acceptance of the wave character of light came many years later when, in 1801, the English physicist and physician Thomas Young (1773–1829) did his now-classic double slit experiment (see Figure 1).

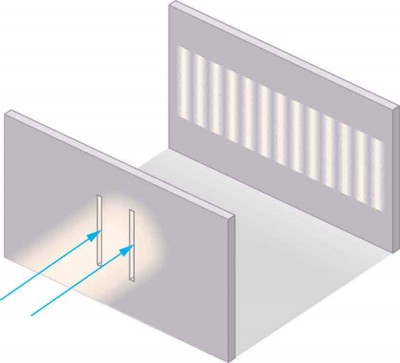
Figure 1. Young’s double slit experiment. Here pure-wavelength light sent through a pair of vertical slits is diffracted into a pattern on the screen of numerous vertical lines spread out horizontally. Without diffraction and interference, the light would simply make two lines on the screen.

Why do we not ordinarily observe wave behavior for light, such as observed in Young’s double slit experiment? First, light must interact with something small, such as the closely spaced slits used by Young, to show pronounced wave effects. Furthermore, Young first passed light from a single source (the Sun) through a single slit to make the light somewhat coherent. By coherent , we mean waves are in phase or have a definite phase relationship. Incoherent means the waves have random phase relationships. Why did Young then pass the light through a double slit? The answer to this question is that two slits provide two coherent light sources that then interfere constructively or destructively. Young used sunlight, where each wavelength forms its own pattern, making the effect more difficult to see. We illustrate the double slit experiment with monochromatic (single λ ) light to clarify the effect. Figure 2 shows the pure constructive and destructive interference of two waves having the same wavelength and amplitude.

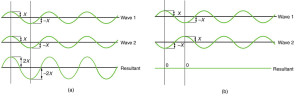
Figure 2. The amplitudes of waves add. (a) Pure constructive interference is obtained when identical waves are in phase. (b) Pure destructive interference occurs when identical waves are exactly out of phase, or shifted by half a wavelength.

When light passes through narrow slits, it is diffracted into semicircular waves, as shown in Figure 3a. Pure constructive interference occurs where the waves are crest to crest or trough to trough. Pure destructive interference occurs where they are crest to trough. The light must fall on a screen and be scattered into our eyes for us to see the pattern. An analogous pattern for water waves is shown in Figure 3b. Note that regions of constructive and destructive interference move out from the slits at well-defined angles to the original beam. These angles depend on wavelength and the distance between the slits, as we shall see below.

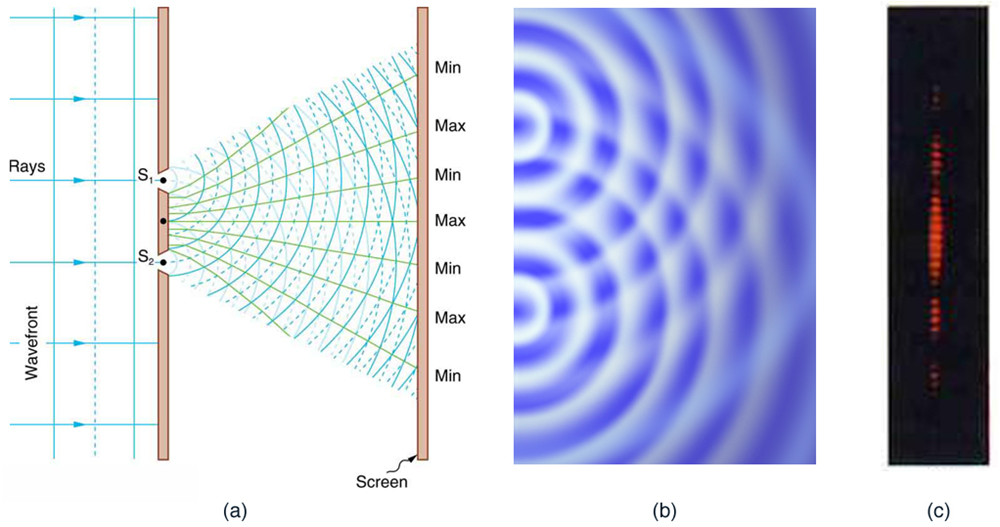
Figure 3. Double slits produce two coherent sources of waves that interfere. (a) Light spreads out (diffracts) from each slit, because the slits are narrow. These waves overlap and interfere constructively (bright lines) and destructively (dark regions). We can only see this if the light falls onto a screen and is scattered into our eyes. (b) Double slit interference pattern for water waves are nearly identical to that for light. Wave action is greatest in regions of constructive interference and least in regions of destructive interference. (c) When light that has passed through double slits falls on a screen, we see a pattern such as this. (credit: PASCO)

To understand the double slit interference pattern, we consider how two waves travel from the slits to the screen, as illustrated in Figure 4. Each slit is a different distance from a given point on the screen. Thus different numbers of wavelengths fit into each path. Waves start out from the slits in phase (crest to crest), but they may end up out of phase (crest to trough) at the screen if the paths differ in length by half a wavelength, interfering destructively as shown in Figure 4a. If the paths differ by a whole wavelength, then the waves arrive in phase (crest to crest) at the screen, interfering constructively as shown in Figure 4b. More generally, if the paths taken by the two waves differ by any half-integral number of wavelengths [(1/2) λ , (3/2) λ , (5/2) λ , etc.], then destructive interference occurs. Similarly, if the paths taken by the two waves differ by any integral number of wavelengths ( λ , 2 λ , 3 λ , etc.), then constructive interference occurs.

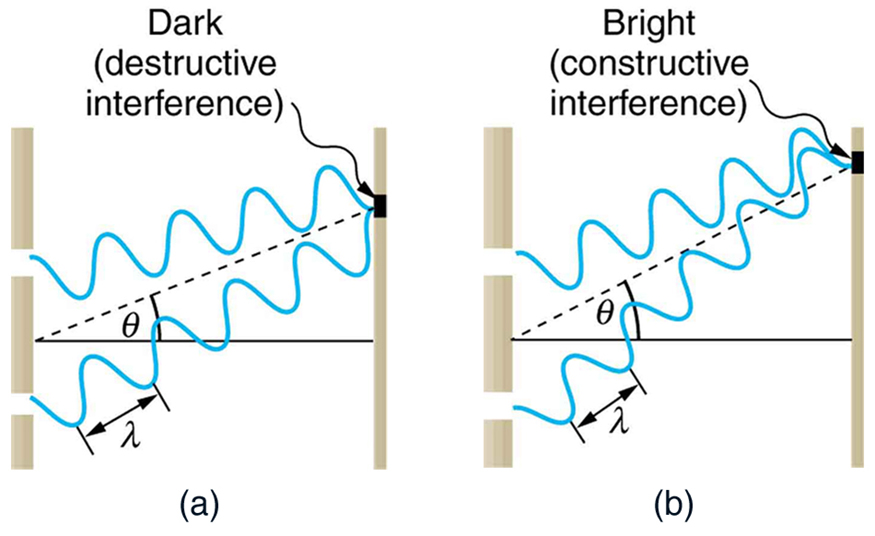
Figure 4. Waves follow different paths from the slits to a common point on a screen. (a) Destructive interference occurs here, because one path is a half wavelength longer than the other. The waves start in phase but arrive out of phase. (b) Constructive interference occurs here because one path is a whole wavelength longer than the other. The waves start out and arrive in phase.

Take-Home Experiment: Using Fingers as Slits

Look at a light, such as a street lamp or incandescent bulb, through the narrow gap between two fingers held close together. What type of pattern do you see? How does it change when you allow the fingers to move a little farther apart? Is it more distinct for a monochromatic source, such as the yellow light from a sodium vapor lamp, than for an incandescent bulb?

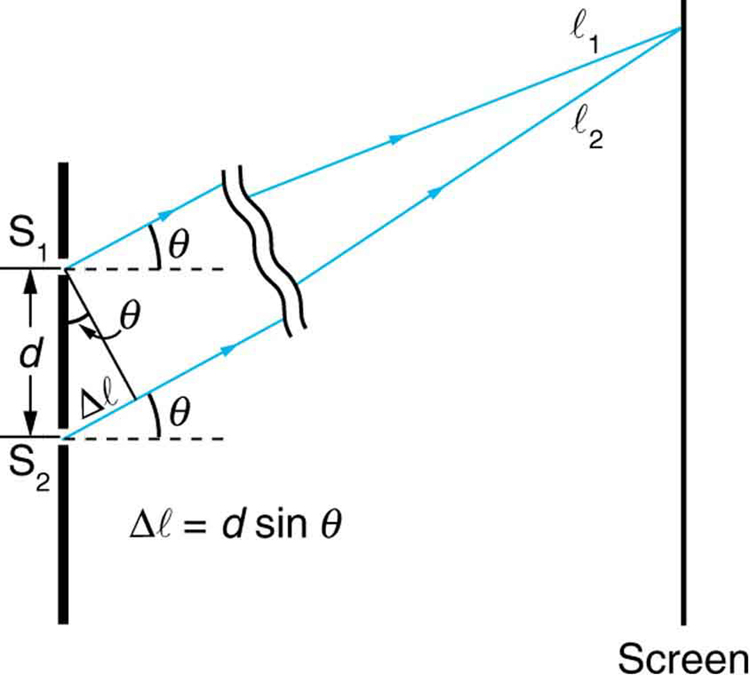
Figure 5. The paths from each slit to a common point on the screen differ by an amount dsinθ, assuming the distance to the screen is much greater than the distance between slits (not to scale here).

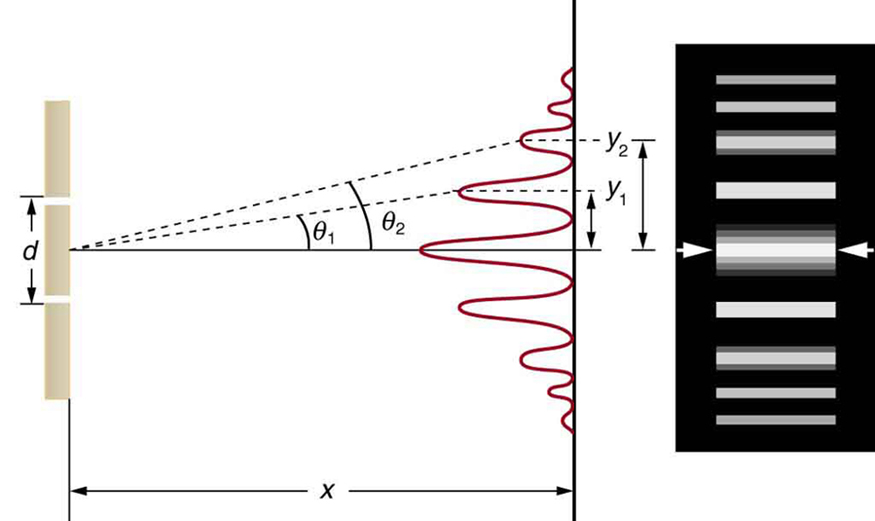
Figure 5 shows how to determine the path length difference for waves traveling from two slits to a common point on a screen. If the screen is a large distance away compared with the distance between the slits, then the angle θ between the path and a line from the slits to the screen (see the figure) is nearly the same for each path. The difference between the paths is shown in the figure; simple trigonometry shows it to be d sin  θ , where d is the distance between the slits. To obtain constructive interference for a double slit , the path length difference must be an integral multiple of the wavelength, or  d sin  θ = mλ, for   m = 0, 1, −1, 2, −2, . . . (constructive).

Similarly, to obtain destructive interference for a double slit , the path length difference must be a half-integral multiple of the wavelength, or

[latex]d\sin\theta=\left(m+\frac{1}{2}\right)\lambda\text{, for }m=0,1,-1,2,-2,\dots\text{ (destructive)}\\[/latex],

where λ is the wavelength of the light, d is the distance between slits, and θ is the angle from the original direction of the beam as discussed above. We call m the order of the interference. For example, m  = 4 is fourth-order interference.

The equations for double slit interference imply that a series of bright and dark lines are formed. For vertical slits, the light spreads out horizontally on either side of the incident beam into a pattern called interference fringes, illustrated in Figure 6. The intensity of the bright fringes falls off on either side, being brightest at the center. The closer the slits are, the more is the spreading of the bright fringes. We can see this by examining the equation  d sin  θ = mλ, for   m = 0, 1, −1, 2, −2, . . . .

For fixed λ and m , the smaller d is, the larger θ must be, since [latex]\sin\theta=\frac{m\lambda}{d}\\[/latex]. This is consistent with our contention that wave effects are most noticeable when the object the wave encounters (here, slits a distance d apart) is small. Small d gives large θ , hence a large effect.

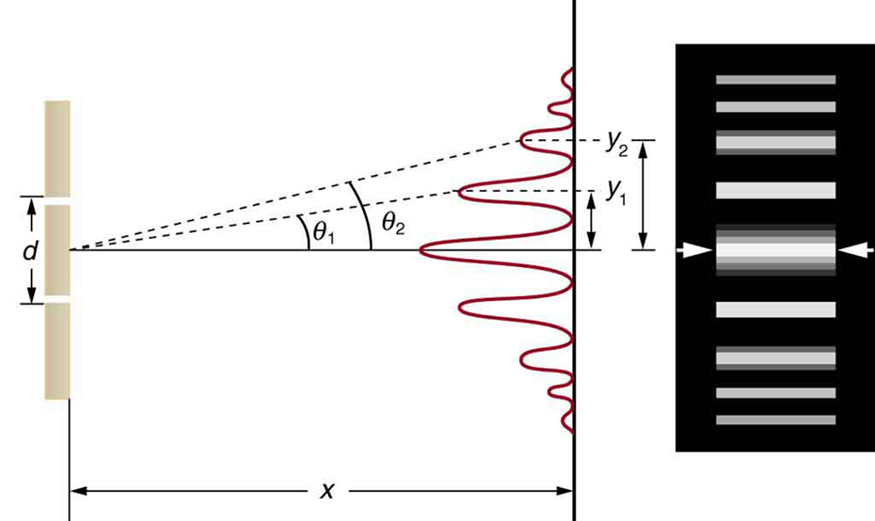
Figure 6. The interference pattern for a double slit has an intensity that falls off with angle. The photograph shows multiple bright and dark lines, or fringes, formed by light passing through a double slit.

Example 1. Finding a Wavelength from an Interference Pattern

Suppose you pass light from a He-Ne laser through two slits separated by 0.0100 mm and find that the third bright line on a screen is formed at an angle of 10.95º relative to the incident beam. What is the wavelength of the light?

The third bright line is due to third-order constructive interference, which means that m  = 3. We are given d = 0.0100 mm and θ  = 10.95º. The wavelength can thus be found using the equation  d sin  θ = mλ  for constructive interference.

The equation is d sin  θ = mλ . Solving for the wavelength λ gives [latex]\lambda=\frac{d\sin\theta}{m}\\[/latex].

Substituting known values yields

[latex]\begin{array}{lll}\lambda&=&\frac{\left(0.0100\text{ nm}\right)\left(\sin10.95^{\circ}\right)}{3}\\\text{ }&=&6.33\times10^{-4}\text{ nm}=633\text{ nm}\end{array}\\[/latex]

To three digits, this is the wavelength of light emitted by the common He-Ne laser. Not by coincidence, this red color is similar to that emitted by neon lights. More important, however, is the fact that interference patterns can be used to measure wavelength. Young did this for visible wavelengths. This analytical technique is still widely used to measure electromagnetic spectra. For a given order, the angle for constructive interference increases with λ , so that spectra (measurements of intensity versus wavelength) can be obtained.

Example 2. Calculating Highest Order Possible

Interference patterns do not have an infinite number of lines, since there is a limit to how big m can be. What is the highest-order constructive interference possible with the system described in the preceding example?

Strategy and Concept

The equation  d sin  θ = mλ ( for   m = 0, 1, −1, 2, −2, . . . ) describes constructive interference. For fixed values of d and λ , the larger m is, the larger sin  θ  is. However, the maximum value that sin  θ  can have is 1, for an angle of 90º. (Larger angles imply that light goes backward and does not reach the screen at all.) Let us find which m corresponds to this maximum diffraction angle.

Solving the equation  d sin  θ = mλ  for m gives [latex]\lambda=\frac{d\sin\theta}{m}\\[/latex].

Taking sin  θ = 1 and substituting the values of d and λ from the preceding example gives

[latex]\displaystyle{m}=\frac{\left(0.0100\text{ mm}\right)\left(1\right)}{633\text{ nm}}\approx15.8\\[/latex]

Therefore, the largest integer m can be is 15, or  m  = 15.

The number of fringes depends on the wavelength and slit separation. The number of fringes will be very large for large slit separations. However, if the slit separation becomes much greater than the wavelength, the intensity of the interference pattern changes so that the screen has two bright lines cast by the slits, as expected when light behaves like a ray. We also note that the fringes get fainter further away from the center. Consequently, not all 15 fringes may be observable.

Section Summary

• Young’s double slit experiment gave definitive proof of the wave character of light.
• An interference pattern is obtained by the superposition of light from two slits.
• There is constructive interference when  d sin  θ = mλ ( for   m = 0, 1, −1, 2, −2, . . . ), where d  is the distance between the slits, θ is the angle relative to the incident direction, and m  is the order of the interference.
• There is destructive interference when  d sin  θ = mλ ( for   m = 0, 1, −1, 2, −2, . . . ).

Conceptual Questions

• Young’s double slit experiment breaks a single light beam into two sources. Would the same pattern be obtained for two independent sources of light, such as the headlights of a distant car? Explain.
• Suppose you use the same double slit to perform Young’s double slit experiment in air and then repeat the experiment in water. Do the angles to the same parts of the interference pattern get larger or smaller? Does the color of the light change? Explain.
• Is it possible to create a situation in which there is only destructive interference? Explain.
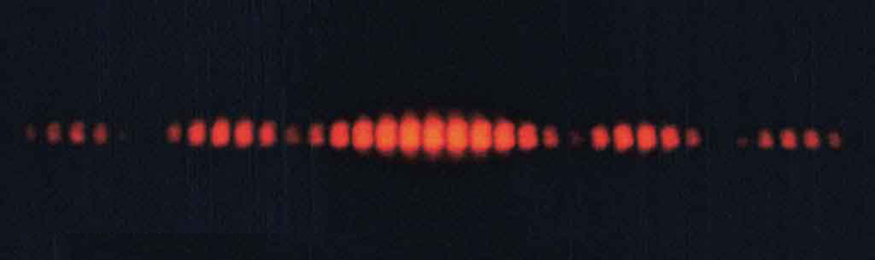
• Figure 7 shows the central part of the interference pattern for a pure wavelength of red light projected onto a double slit. The pattern is actually a combination of single slit and double slit interference. Note that the bright spots are evenly spaced. Is this a double slit or single slit characteristic? Note that some of the bright spots are dim on either side of the center. Is this a single slit or double slit characteristic? Which is smaller, the slit width or the separation between slits? Explain your responses.

Figure 7. This double slit interference pattern also shows signs of single slit interference. (credit: PASCO)

Problems & Exercises

• At what angle is the first-order maximum for 450-nm wavelength blue light falling on double slits separated by 0.0500 mm?
• Calculate the angle for the third-order maximum of 580-nm wavelength yellow light falling on double slits separated by 0.100 mm.
• What is the separation between two slits for which 610-nm orange light has its first maximum at an angle of 30.0º?
• Find the distance between two slits that produces the first minimum for 410-nm violet light at an angle of 45.0º.
• Calculate the wavelength of light that has its third minimum at an angle of 30.0º when falling on double slits separated by 3.00 μm.
• What is the wavelength of light falling on double slits separated by 2.00 μm if the third-order maximum is at an angle of 60.0º?
• At what angle is the fourth-order maximum for the situation in Question 1?
• What is the highest-order maximum for 400-nm light falling on double slits separated by 25.0 μm?
• Find the largest wavelength of light falling on double slits separated by 1.20 μm for which there is a first-order maximum. Is this in the visible part of the spectrum?
• What is the smallest separation between two slits that will produce a second-order maximum for 720-nm red light?
• (a) What is the smallest separation between two slits that will produce a second-order maximum for any visible light? (b) For all visible light?
• (a) If the first-order maximum for pure-wavelength light falling on a double slit is at an angle of 10.0º, at what angle is the second-order maximum? (b) What is the angle of the first minimum? (c) What is the highest-order maximum possible here?

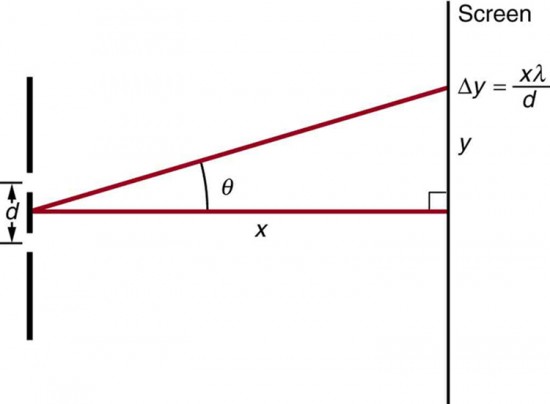
Figure 8. The distance between adjacent fringes is [latex]\Delta{y}=\frac{x\lambda}{d}\\[/latex], assuming the slit separation d  is large compared with λ .

• Using the result of the problem above, calculate the distance between fringes for 633-nm light falling on double slits separated by 0.0800 mm, located 3.00 m from a screen as in Figure 8.
• Using the result of the problem two problems prior, find the wavelength of light that produces fringes 7.50 mm apart on a screen 2.00 m from double slits separated by 0.120 mm (see Figure 8).

coherent:  waves are in phase or have a definite phase relationship

constructive interference for a double slit:  the path length difference must be an integral multiple of the wavelength

destructive interference for a double slit:  the path length difference must be a half-integral multiple of the wavelength

incoherent:  waves have random phase relationships

order:  the integer m  used in the equations for constructive and destructive interference for a double slit

Selected Solutions to Problems & Exercises

3. 1.22 × 10 −6 m

9. 1200 nm (not visible)

11. (a) 760 nm; (b) 1520 nm

13. For small angles sin θ − tan θ  ≈ θ  (in radians).

For two adjacent fringes we have,  d  sin θ m = mλ  and  d sin θ m + 1 = ( m  + 1) λ

Subtracting these equations gives

[latex]\begin{array}{}d\left(\sin{\theta }_{\text{m}+1}-\sin{\theta }_{\text{m}}\right)=\left[\left(m+1\right)-m\right]\lambda \\ d\left({\theta }_{\text{m}+1}-{\theta }_{\text{m}}\right)=\lambda \\ \text{tan}{\theta }_{\text{m}}=\frac{{y}_{\text{m}}}{x}\approx {\theta }_{\text{m}}\Rightarrow d\left(\frac{{y}_{\text{m}+1}}{x}-\frac{{y}_{\text{m}}}{x}\right)=\lambda \\ d\frac{\Delta y}{x}=\lambda \Rightarrow \Delta y=\frac{\mathrm{x\lambda }}{d}\end{array}\\[/latex]

Candela Citations

• College Physics. Authored by : OpenStax College. Located at : http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a/College_Physics . License : CC BY: Attribution . License Terms : Located at License

Browse Course Material

Course info.

• Prof. David Kaiser

Departments

• Science, Technology, and Society

As Taught In

• History of Science and Technology
• Modern History

Learning Resource Types

Einstein, oppenheimer, feynman: physics in the 20th century, lecture notes: the double-slit experiment: an adventure in three acts.

You are leaving MIT OpenCourseWare

Chapter 27 Wave Optics

27.3 Young’s Double Slit Experiment

• Explain the phenomena of interference.
• Define constructive interference for a double slit and destructive interference for a double slit.

Although Christiaan Huygens thought that light was a wave, Isaac Newton did not. Newton felt that there were other explanations for color, and for the interference and diffraction effects that were observable at the time. Owing to Newton’s tremendous stature, his view generally prevailed. The fact that Huygens’s principle worked was not considered evidence that was direct enough to prove that light is a wave. The acceptance of the wave character of light came many years later when, in 1801, the English physicist and physician Thomas Young (1773–1829) did his now-classic double slit experiment (see Figure 1 ).

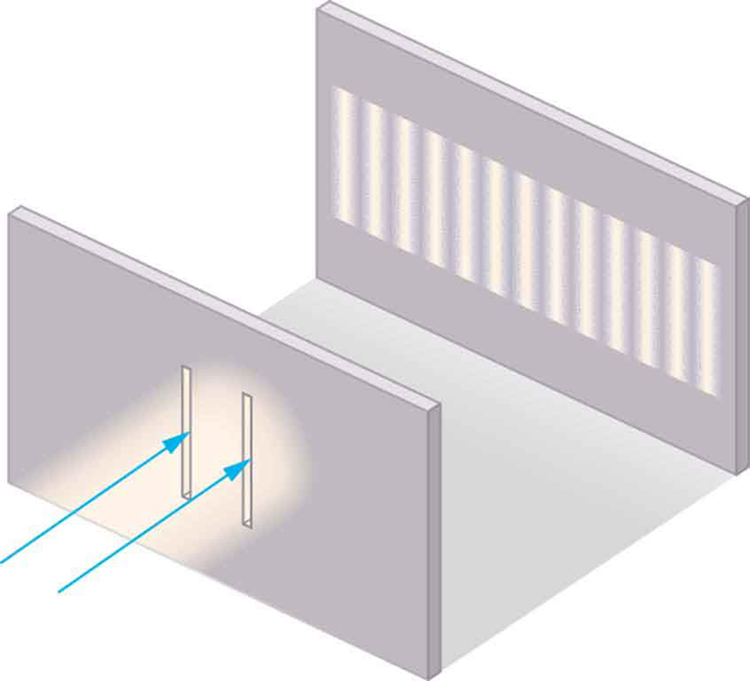
Why do we not ordinarily observe wave behavior for light, such as observed in Young’s double slit experiment? First, light must interact with something small, such as the closely spaced slits used by Young, to show pronounced wave effects. Furthermore, Young first passed light from a single source (the Sun) through a single slit to make the light somewhat coherent. By coherent , we mean waves are in phase or have a definite phase relationship. Incoherent means the waves have random phase relationships. Why did Young then pass the light through a double slit? The answer to this question is that two slits provide two coherent light sources that then interfere constructively or destructively. Young used sunlight, where each wavelength forms its own pattern, making the effect more difficult to see. We illustrate the double slit experiment with monochromatic (single [latex]{\lambda}[/latex]) light to clarify the effect. Figure 2 shows the pure constructive and destructive interference of two waves having the same wavelength and amplitude.

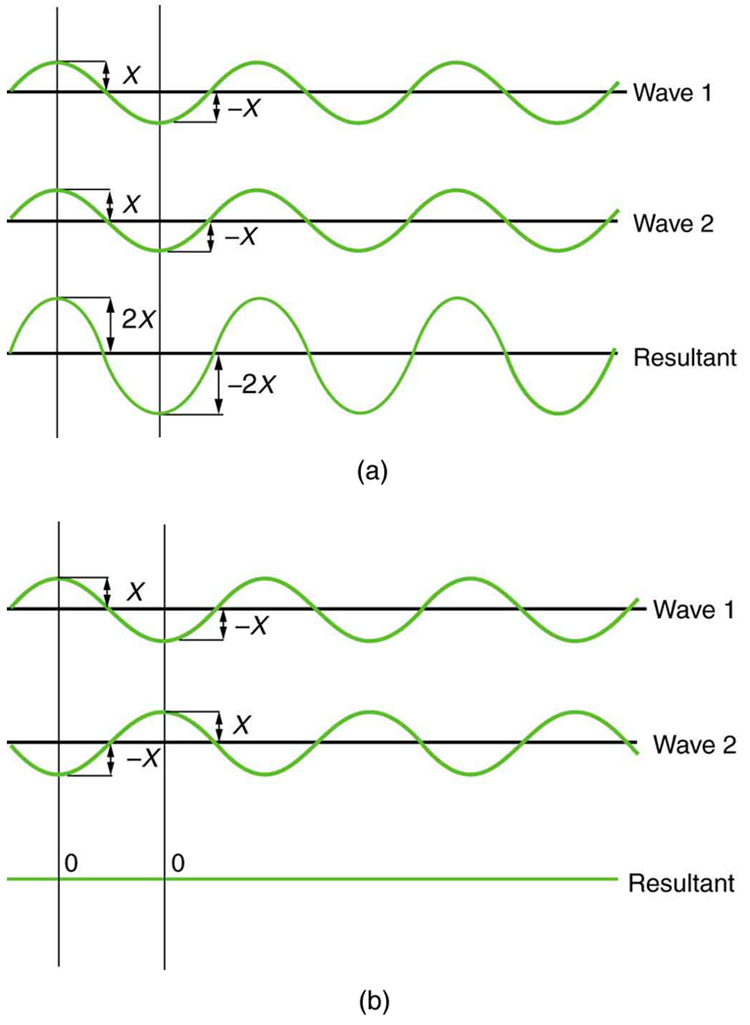
When light passes through narrow slits, it is diffracted into semicircular waves, as shown in Figure 3 (a). Pure constructive interference occurs where the waves are crest to crest or trough to trough. Pure destructive interference occurs where they are crest to trough. The light must fall on a screen and be scattered into our eyes for us to see the pattern. An analogous pattern for water waves is shown in Figure 3 (b). Note that regions of constructive and destructive interference move out from the slits at well-defined angles to the original beam. These angles depend on wavelength and the distance between the slits, as we shall see below.

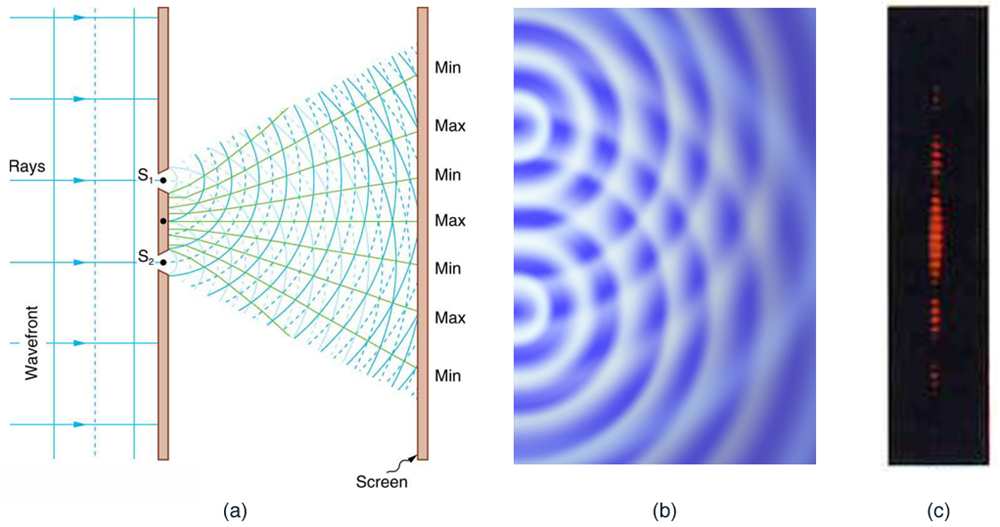
To understand the double slit interference pattern, we consider how two waves travel from the slits to the screen, as illustrated in Figure 4 . Each slit is a different distance from a given point on the screen. Thus different numbers of wavelengths fit into each path. Waves start out from the slits in phase (crest to crest), but they may end up out of phase (crest to trough) at the screen if the paths differ in length by half a wavelength, interfering destructively as shown in Figure 4 (a). If the paths differ by a whole wavelength, then the waves arrive in phase (crest to crest) at the screen, interfering constructively as shown in Figure 4 (b). More generally, if the paths taken by the two waves differ by any half-integral number of wavelengths [[latex]{(1/2) \;\lambda}[/latex], [latex]{(3/2) \;\lambda}[/latex], [latex]{(5/2) \;\lambda}[/latex], etc.], then destructive interference occurs. Similarly, if the paths taken by the two waves differ by any integral number of wavelengths ([latex]{\lambda}[/latex], [latex]{2 \lambda}[/latex], [latex]{3 \lambda}[/latex], etc.), then constructive interference occurs.

Take-Home Experiment: Using Fingers as Slits

Look at a light, such as a street lamp or incandescent bulb, through the narrow gap between two fingers held close together. What type of pattern do you see? How does it change when you allow the fingers to move a little farther apart? Is it more distinct for a monochromatic source, such as the yellow light from a sodium vapor lamp, than for an incandescent bulb?

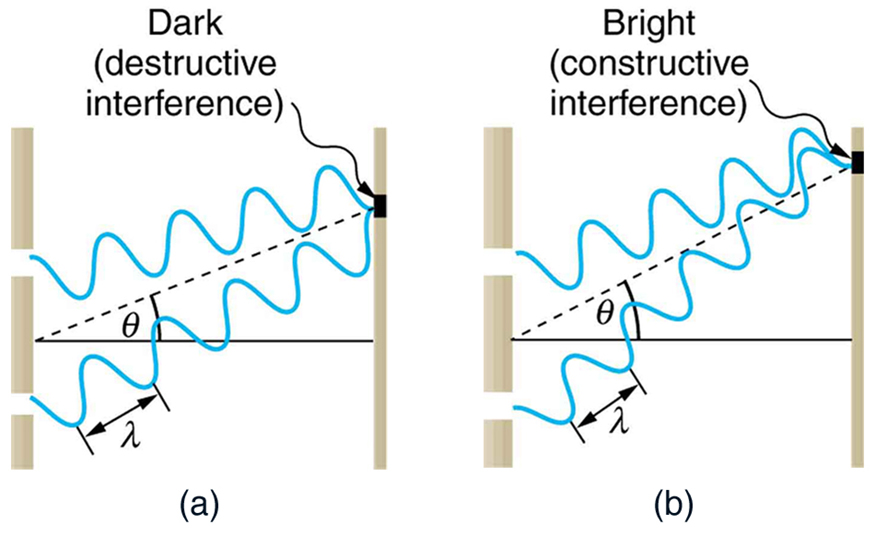
Figure 5 shows how to determine the path length difference for waves traveling from two slits to a common point on a screen. If the screen is a large distance away compared with the distance between the slits, then the angle [latex]{\theta}[/latex] between the path and a line from the slits to the screen (see the figure) is nearly the same for each path. The difference between the paths is shown in the figure; simple trigonometry shows it to be [latex]{d \;\text{sin} \;\theta}[/latex], where [latex]{d}[/latex] is the distance between the slits. To obtain constructive interference for a double slit , the path length difference must be an integral multiple of the wavelength, or

Similarly, to obtain destructive interference for a double slit , the path length difference must be a half-integral multiple of the wavelength, or

where [latex]{\lambda}[/latex] is the wavelength of the light, [latex]{d}[/latex] is the distance between slits, and [latex]{\theta}[/latex] is the angle from the original direction of the beam as discussed above. We call [latex]{m}[/latex] the order of the interference. For example, [latex]{m = 4}[/latex] is fourth-order interference.

The equations for double slit interference imply that a series of bright and dark lines are formed. For vertical slits, the light spreads out horizontally on either side of the incident beam into a pattern called interference fringes, illustrated in Figure 6 . The intensity of the bright fringes falls off on either side, being brightest at the center. The closer the slits are, the more is the spreading of the bright fringes. We can see this by examining the equation

For fixed [latex]{\lambda}[/latex] and [latex]{m}[/latex], the smaller [latex]{d}[/latex] is, the larger [latex]{\theta}[/latex] must be, since [latex]{\text{sin} \;\theta = m \lambda / d}[/latex].

This is consistent with our contention that wave effects are most noticeable when the object the wave encounters (here, slits a distance [latex]{d}[/latex] apart) is small. Small [latex]{d}[/latex] gives large [latex]{\theta}[/latex], hence a large effect.

Example 1: Finding a Wavelength from an Interference Pattern

Suppose you pass light from a He-Ne laser through two slits separated by 0.0100 mm and find that the third bright line on a screen is formed at an angle of [latex]{10.95 ^{\circ}}[/latex] relative to the incident beam. What is the wavelength of the light?

The third bright line is due to third-order constructive interference, which means that [latex]{m = 3}[/latex]. We are given [latex]{d = 0.0100 \;\text{mm}}[/latex] and [latex]{\theta = 10.95^{\circ}}[/latex]. The wavelength can thus be found using the equation [latex]{d \;\text{sin} \;\theta = m \lambda}[/latex] for constructive interference.

The equation is [latex]{d \;\text{sin} \;\theta = m \lambda}[/latex]. Solving for the wavelength [latex]{\lambda}[/latex] gives

Substituting known values yields

To three digits, this is the wavelength of light emitted by the common He-Ne laser. Not by coincidence, this red color is similar to that emitted by neon lights. More important, however, is the fact that interference patterns can be used to measure wavelength. Young did this for visible wavelengths. This analytical technique is still widely used to measure electromagnetic spectra. For a given order, the angle for constructive interference increases with [latex]{\lambda}[/latex], so that spectra (measurements of intensity versus wavelength) can be obtained.

Example 2: Calculating Highest Order Possible

Interference patterns do not have an infinite number of lines, since there is a limit to how big [latex]{m}[/latex] can be. What is the highest-order constructive interference possible with the system described in the preceding example?

Strategy and Concept

The equation [latex]{d \;\text{sin} \;\theta = m \lambda \; (\text{for} \; m = 0, \; 1, \; -1, \; 2, \; -2, \; \dots)}[/latex] describes constructive interference. For fixed values of [latex]{d}[/latex] and [latex]{\lambda}[/latex], the larger [latex]{m}[/latex] is, the larger [latex]{\text{sin} \;\theta}[/latex] is. However, the maximum value that [latex]{\text{sin} \;\theta}[/latex] can have is 1, for an angle of [latex]{90 ^{\circ}}[/latex]. (Larger angles imply that light goes backward and does not reach the screen at all.) Let us find which [latex]{m}[/latex] corresponds to this maximum diffraction angle.

Solving the equation [latex]{d \;\text{sin} \;\theta = m \lambda}[/latex] for [latex]{m}[/latex] gives

Taking [latex]{\text{sin} \;\theta = 1}[/latex] and substituting the values of [latex]{d}[/latex] and [latex]{\lambda}[/latex] from the preceding example gives

Therefore, the largest integer [latex]{m}[/latex] can be is 15, or

The number of fringes depends on the wavelength and slit separation. The number of fringes will be very large for large slit separations. However, if the slit separation becomes much greater than the wavelength, the intensity of the interference pattern changes so that the screen has two bright lines cast by the slits, as expected when light behaves like a ray. We also note that the fringes get fainter further away from the center. Consequently, not all 15 fringes may be observable.

Section Summary

• Young’s double slit experiment gave definitive proof of the wave character of light.
• An interference pattern is obtained by the superposition of light from two slits.
• There is constructive interference when [latex]{d \;\text{sin} \;\theta = m \lambda \;(\text{for} \; m = 0, \; 1, \; -1, \;2, \; -2, \dots)}[/latex], where [latex]{d}[/latex] is the distance between the slits, [latex]{\theta}[/latex] is the angle relative to the incident direction, and [latex]{m}[/latex] is the order of the interference.
• There is destructive interference when [latex]{d \;\text{sin} \;\theta = (m+ \frac{1}{2}) \lambda}[/latex] (for [latex]{m = 0, \; 1, \; -1, \; 2, \; -2, \; \dots}[/latex]).

Conceptual Questions

1: Young’s double slit experiment breaks a single light beam into two sources. Would the same pattern be obtained for two independent sources of light, such as the headlights of a distant car? Explain.

2: Suppose you use the same double slit to perform Young’s double slit experiment in air and then repeat the experiment in water. Do the angles to the same parts of the interference pattern get larger or smaller? Does the color of the light change? Explain.

3: Is it possible to create a situation in which there is only destructive interference? Explain.

4:   Figure 7 shows the central part of the interference pattern for a pure wavelength of red light projected onto a double slit. The pattern is actually a combination of single slit and double slit interference. Note that the bright spots are evenly spaced. Is this a double slit or single slit characteristic? Note that some of the bright spots are dim on either side of the center. Is this a single slit or double slit characteristic? Which is smaller, the slit width or the separation between slits? Explain your responses.

Problems & Exercises

2: Calculate the angle for the third-order maximum of 580-nm wavelength yellow light falling on double slits separated by 0.100 mm.

3: What is the separation between two slits for which 610-nm orange light has its first maximum at an angle of [latex]{30.0 ^{\circ}}[/latex]?

4: Find the distance between two slits that produces the first minimum for 410-nm violet light at an angle of [latex]{45.0 ^{\circ}}[/latex].

5: Calculate the wavelength of light that has its third minimum at an angle of [latex]{30.0 ^{\circ}}[/latex] when falling on double slits separated by [latex]{3.00 \;\mu \text{m}}[/latex]. Explicitly, show how you follow the steps in Chapter 27.7 Problem-Solving Strategies for Wave Optics .

6: What is the wavelength of light falling on double slits separated by [latex]{2.00 \;\mu \text{m}}[/latex] if the third-order maximum is at an angle of [latex]{60.0 ^{\circ}}[/latex]?

7: At what angle is the fourth-order maximum for the situation in Problems & Exercises 1 ?

8: What is the highest-order maximum for 400-nm light falling on double slits separated by [latex]{25.0 \;\mu \text{m}}[/latex]?

9: Find the largest wavelength of light falling on double slits separated by [latex]{1.20 \;\mu \text{m}}[/latex] for which there is a first-order maximum. Is this in the visible part of the spectrum?

10: What is the smallest separation between two slits that will produce a second-order maximum for 720-nm red light?

11: (a) What is the smallest separation between two slits that will produce a second-order maximum for any visible light? (b) For all visible light?

12: (a) If the first-order maximum for pure-wavelength light falling on a double slit is at an angle of [latex]{10.0^{\circ}}[/latex], at what angle is the second-order maximum? (b) What is the angle of the first minimum? (c) What is the highest-order maximum possible here?

13:   Figure 8 shows a double slit located a distance [latex]{x}[/latex] from a screen, with the distance from the center of the screen given by [latex]{y}[/latex]. When the distance [latex]{d}[/latex] between the slits is relatively large, there will be numerous bright spots, called fringes. Show that, for small angles (where [latex]{\text{sin} \;\theta \approx \theta}[/latex], with [latex]{\theta}[/latex] in radians), the distance between fringes is given by [latex]{\Delta y = x \lambda /d}[/latex].

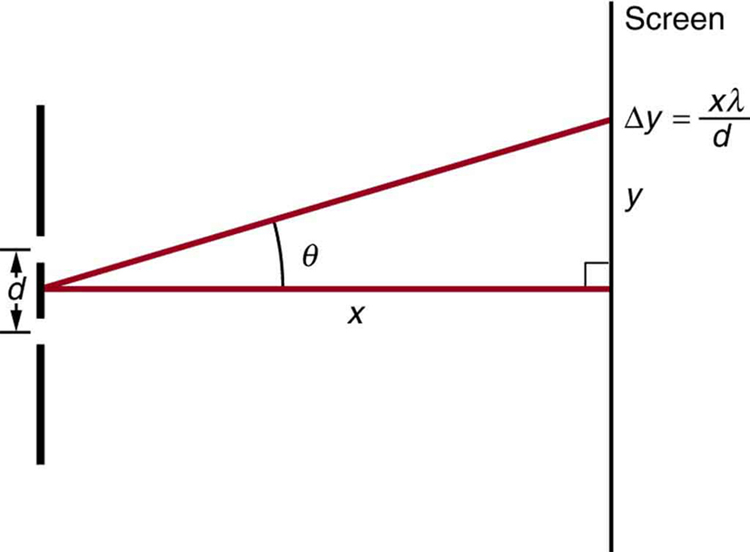
14: Using the result of the problem above, calculate the distance between fringes for 633-nm light falling on double slits separated by 0.0800 mm, located 3.00 m from a screen as in Figure 8 .

15: Using the result of the problem two problems prior, find the wavelength of light that produces fringes 7.50 mm apart on a screen 2.00 m from double slits separated by 0.120 mm (see Figure 8 ).

1:  [latex]{0.516 ^{\circ}}[/latex]

3:  [latex]{1.22 \times 10^{-6} \;\text{m}}[/latex]

7: [latex]{2.06 ^{\circ}}[/latex]

9: 1200 nm (not visible)

11: (a) 760 nm

(b) 1520 nm

13: For small angles [latex]{\text{sin} \;\theta - \;\text{tan} \;\theta \approx \theta}[/latex] (in radians).

For two adjacent fringes we have,

Subtracting these equations gives

College Physics Copyright © August 22, 2016 by OpenStax is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book