two independent variable experiment

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

8.2 Multiple Independent Variables

Learning objectives.

• Explain why researchers often include multiple independent variables in their studies.
• Define factorial design, and use a factorial design table to represent and interpret simple factorial designs.
• Distinguish between main effects and interactions, and recognize and give examples of each.
• Sketch and interpret bar graphs and line graphs showing the results of studies with simple factorial designs.

Just as it is common for studies in psychology to include multiple dependent variables, it is also common for them to include multiple independent variables. Schnall and her colleagues studied the effect of both disgust and private body consciousness in the same study. Researchers’ inclusion of multiple independent variables in one experiment is further illustrated by the following actual titles from various professional journals:

• The Effects of Temporal Delay and Orientation on Haptic Object Recognition
• Opening Closed Minds: The Combined Effects of Intergroup Contact and Need for Closure on Prejudice
• Effects of Expectancies and Coping on Pain-Induced Intentions to Smoke
• The Effect of Age and Divided Attention on Spontaneous Recognition
• The Effects of Reduced Food Size and Package Size on the Consumption Behavior of Restrained and Unrestrained Eaters

Just as including multiple dependent variables in the same experiment allows one to answer more research questions, so too does including multiple independent variables in the same experiment. For example, instead of conducting one study on the effect of disgust on moral judgment and another on the effect of private body consciousness on moral judgment, Schnall and colleagues were able to conduct one study that addressed both questions. But including multiple independent variables also allows the researcher to answer questions about whether the effect of one independent variable depends on the level of another. This is referred to as an interaction between the independent variables. Schnall and her colleagues, for example, observed an interaction between disgust and private body consciousness because the effect of disgust depended on whether participants were high or low in private body consciousness. As we will see, interactions are often among the most interesting results in psychological research.

Factorial Designs

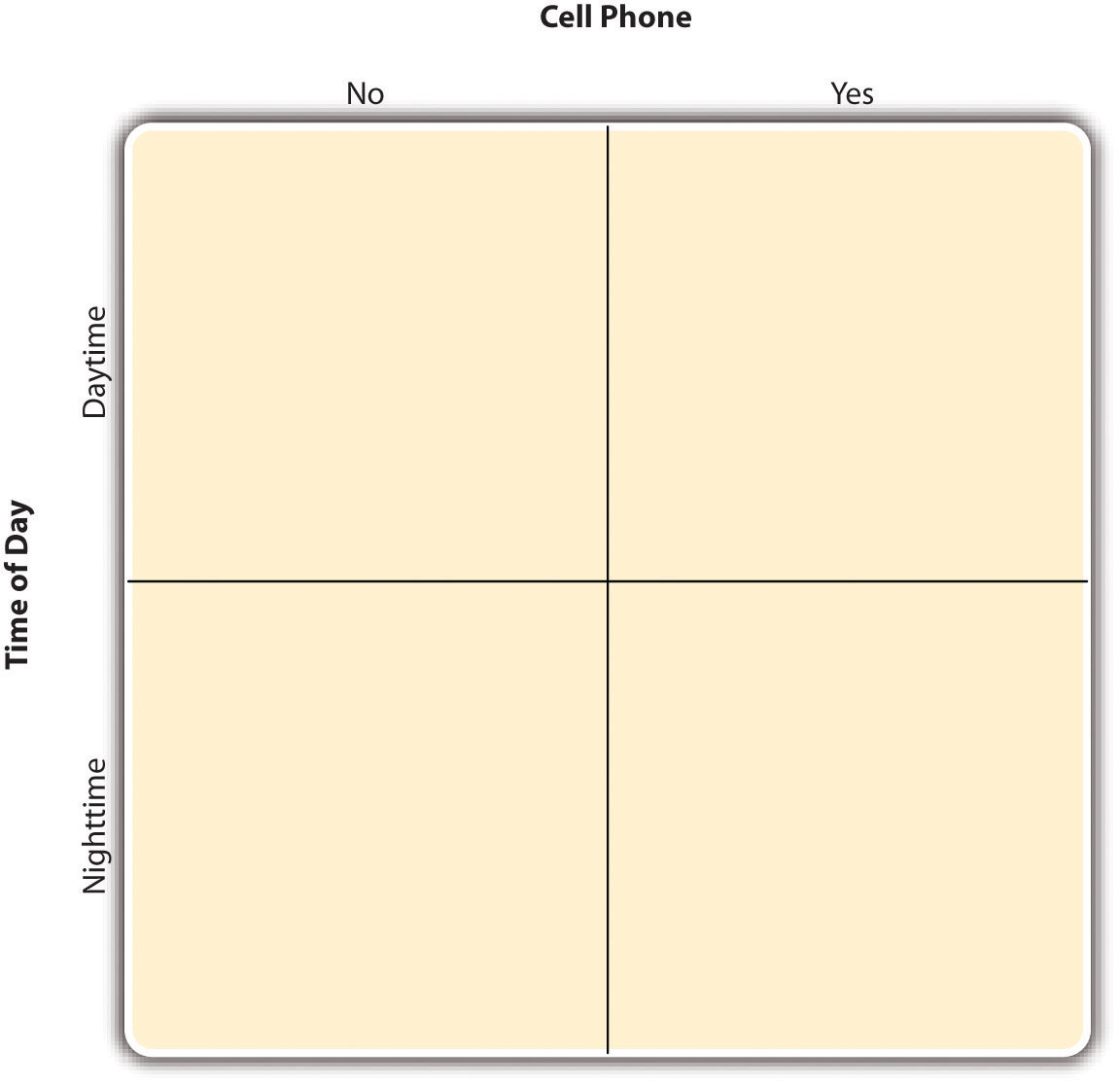
By far the most common approach to including multiple independent variables in an experiment is the factorial design. In a factorial design , each level of one independent variable (which can also be called a factor ) is combined with each level of the others to produce all possible combinations. Each combination, then, becomes a condition in the experiment. Imagine, for example, an experiment on the effect of cell phone use (yes vs. no) and time of day (day vs. night) on driving ability. This is shown in the factorial design table in Figure 8.2 “Factorial Design Table Representing a 2 × 2 Factorial Design” . The columns of the table represent cell phone use, and the rows represent time of day. The four cells of the table represent the four possible combinations or conditions: using a cell phone during the day, not using a cell phone during the day, using a cell phone at night, and not using a cell phone at night. This particular design is a 2 × 2 (read “two-by-two”) factorial design because it combines two variables, each of which has two levels. If one of the independent variables had a third level (e.g., using a handheld cell phone, using a hands-free cell phone, and not using a cell phone), then it would be a 3 × 2 factorial design, and there would be six distinct conditions. Notice that the number of possible conditions is the product of the numbers of levels. A 2 × 2 factorial design has four conditions, a 3 × 2 factorial design has six conditions, a 4 × 5 factorial design would have 20 conditions, and so on.

Figure 8.2 Factorial Design Table Representing a 2 × 2 Factorial Design

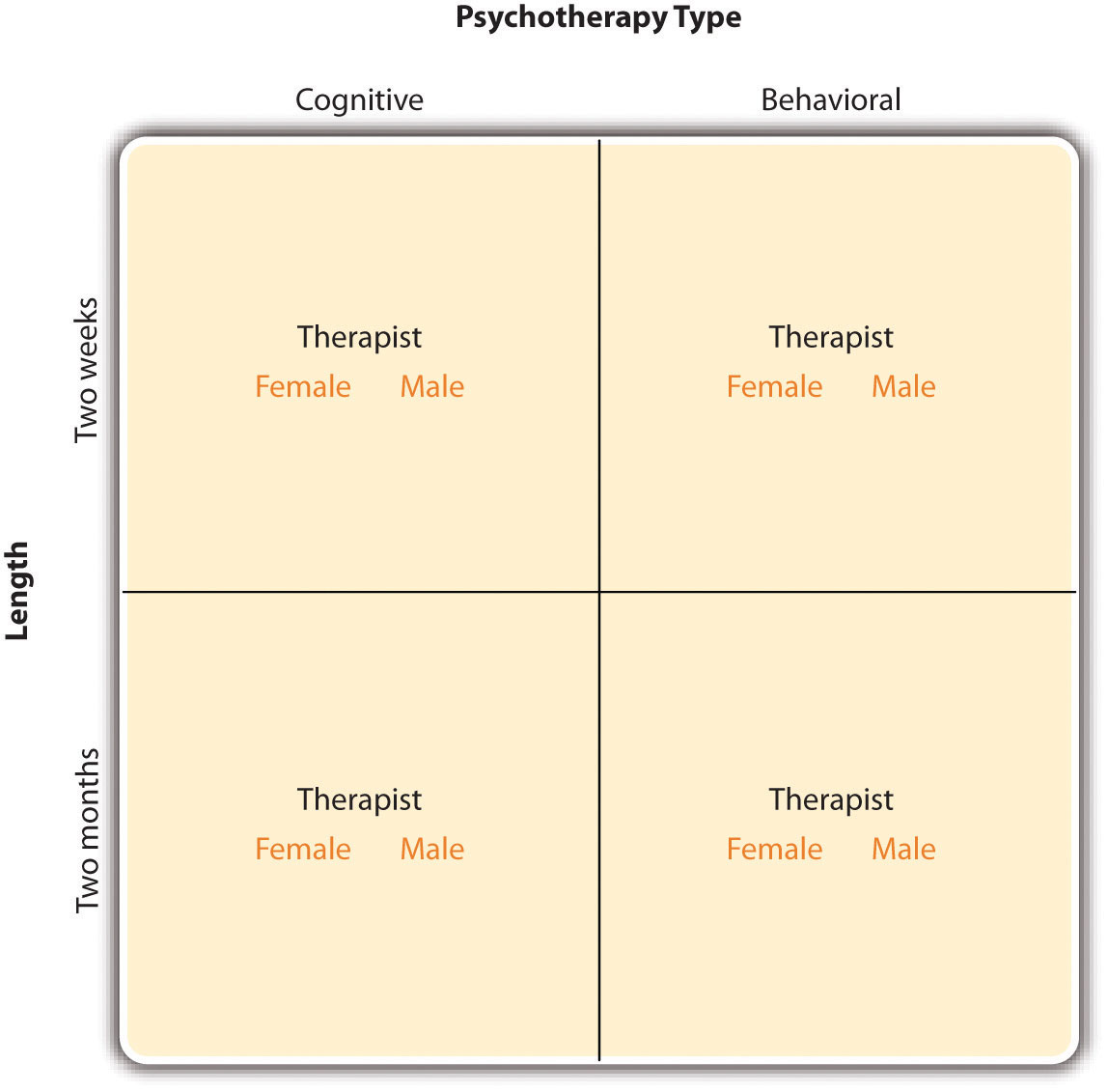
In principle, factorial designs can include any number of independent variables with any number of levels. For example, an experiment could include the type of psychotherapy (cognitive vs. behavioral), the length of the psychotherapy (2 weeks vs. 2 months), and the sex of the psychotherapist (female vs. male). This would be a 2 × 2 × 2 factorial design and would have eight conditions. Figure 8.3 “Factorial Design Table Representing a 2 × 2 × 2 Factorial Design” shows one way to represent this design. In practice, it is unusual for there to be more than three independent variables with more than two or three levels each because the number of conditions can quickly become unmanageable. For example, adding a fourth independent variable with three levels (e.g., therapist experience: low vs. medium vs. high) to the current example would make it a 2 × 2 × 2 × 3 factorial design with 24 distinct conditions. In the rest of this section, we will focus on designs with two independent variables. The general principles discussed here extend in a straightforward way to more complex factorial designs.

Figure 8.3 Factorial Design Table Representing a 2 × 2 × 2 Factorial Design

Assigning Participants to Conditions

Recall that in a simple between-subjects design, each participant is tested in only one condition. In a simple within-subjects design, each participant is tested in all conditions. In a factorial experiment, the decision to take the between-subjects or within-subjects approach must be made separately for each independent variable. In a between-subjects factorial design , all of the independent variables are manipulated between subjects. For example, all participants could be tested either while using a cell phone or while not using a cell phone and either during the day or during the night. This would mean that each participant was tested in one and only one condition. In a within-subjects factorial design , all of the independent variables are manipulated within subjects. All participants could be tested both while using a cell phone and while not using a cell phone and both during the day and during the night. This would mean that each participant was tested in all conditions. The advantages and disadvantages of these two approaches are the same as those discussed in Chapter 6 “Experimental Research” . The between-subjects design is conceptually simpler, avoids carryover effects, and minimizes the time and effort of each participant. The within-subjects design is more efficient for the researcher and controls extraneous participant variables.

It is also possible to manipulate one independent variable between subjects and another within subjects. This is called a mixed factorial design . For example, a researcher might choose to treat cell phone use as a within-subjects factor by testing the same participants both while using a cell phone and while not using a cell phone (while counterbalancing the order of these two conditions). But he or she might choose to treat time of day as a between-subjects factor by testing each participant either during the day or during the night (perhaps because this only requires them to come in for testing once). Thus each participant in this mixed design would be tested in two of the four conditions.

Regardless of whether the design is between subjects, within subjects, or mixed, the actual assignment of participants to conditions or orders of conditions is typically done randomly.

Nonmanipulated Independent Variables

In many factorial designs, one of the independent variables is a nonmanipulated independent variable . The researcher measures it but does not manipulate it. The study by Schnall and colleagues is a good example. One independent variable was disgust, which the researchers manipulated by testing participants in a clean room or a messy room. The other was private body consciousness, which the researchers simply measured. Another example is a study by Halle Brown and colleagues in which participants were exposed to several words that they were later asked to recall (Brown, Kosslyn, Delamater, Fama, & Barsky, 1999). The manipulated independent variable was the type of word. Some were negative health-related words (e.g., tumor , coronary ), and others were not health related (e.g., election , geometry ). The nonmanipulated independent variable was whether participants were high or low in hypochondriasis (excessive concern with ordinary bodily symptoms). The result of this study was that the participants high in hypochondriasis were better than those low in hypochondriasis at recalling the health-related words, but they were no better at recalling the non-health-related words.

Such studies are extremely common, and there are several points worth making about them. First, nonmanipulated independent variables are usually participant variables (private body consciousness, hypochondriasis, self-esteem, and so on), and as such they are by definition between-subjects factors. For example, people are either low in hypochondriasis or high in hypochondriasis; they cannot be tested in both of these conditions. Second, such studies are generally considered to be experiments as long as at least one independent variable is manipulated, regardless of how many nonmanipulated independent variables are included. Third, it is important to remember that causal conclusions can only be drawn about the manipulated independent variable. For example, Schnall and her colleagues were justified in concluding that disgust affected the harshness of their participants’ moral judgments because they manipulated that variable and randomly assigned participants to the clean or messy room. But they would not have been justified in concluding that participants’ private body consciousness affected the harshness of their participants’ moral judgments because they did not manipulate that variable. It could be, for example, that having a strict moral code and a heightened awareness of one’s body are both caused by some third variable (e.g., neuroticism). Thus it is important to be aware of which variables in a study are manipulated and which are not.

Graphing the Results of Factorial Experiments

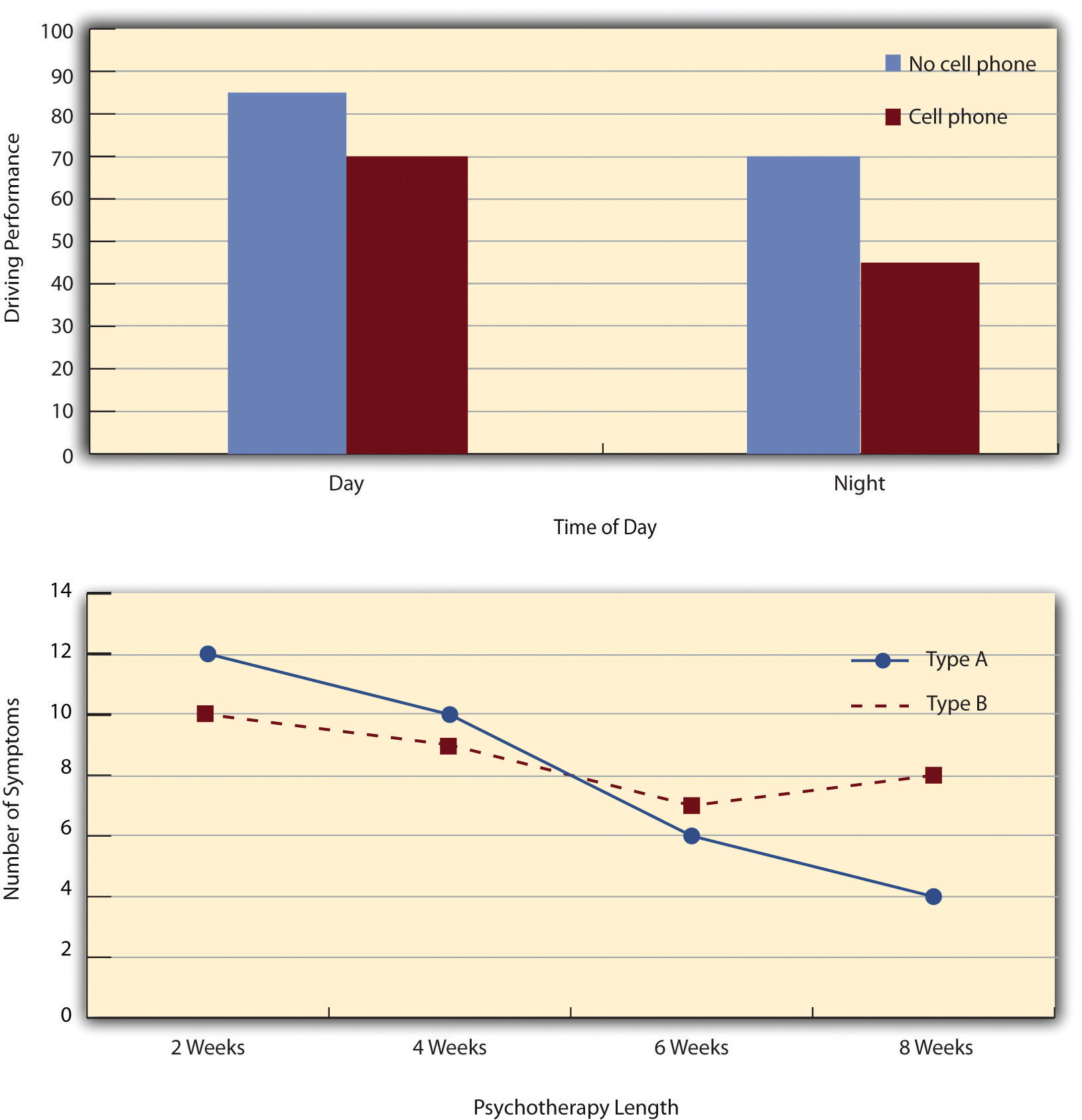
The results of factorial experiments with two independent variables can be graphed by representing one independent variable on the x- axis and representing the other by using different kinds of bars or lines. (The y- axis is always reserved for the dependent variable.) Figure 8.4 “Two Ways to Plot the Results of a Factorial Experiment With Two Independent Variables” shows results for two hypothetical factorial experiments. The top panel shows the results of a 2 × 2 design. Time of day (day vs. night) is represented by different locations on the x- axis, and cell phone use (no vs. yes) is represented by different-colored bars. (It would also be possible to represent cell phone use on the x- axis and time of day as different-colored bars. The choice comes down to which way seems to communicate the results most clearly.) The bottom panel of Figure 8.4 “Two Ways to Plot the Results of a Factorial Experiment With Two Independent Variables” shows the results of a 4 × 2 design in which one of the variables is quantitative. This variable, psychotherapy length, is represented along the x- axis, and the other variable (psychotherapy type) is represented by differently formatted lines. This is a line graph rather than a bar graph because the variable on the x- axis is quantitative with a small number of distinct levels.

Figure 8.4 Two Ways to Plot the Results of a Factorial Experiment With Two Independent Variables

Main Effects and Interactions

In factorial designs, there are two kinds of results that are of interest: main effects and interaction effects (which are also called just “interactions”). A main effect is the statistical relationship between one independent variable and a dependent variable—averaging across the levels of the other independent variable. Thus there is one main effect to consider for each independent variable in the study. The top panel of Figure 8.4 “Two Ways to Plot the Results of a Factorial Experiment With Two Independent Variables” shows a main effect of cell phone use because driving performance was better, on average, when participants were not using cell phones than when they were. The blue bars are, on average, higher than the red bars. It also shows a main effect of time of day because driving performance was better during the day than during the night—both when participants were using cell phones and when they were not. Main effects are independent of each other in the sense that whether or not there is a main effect of one independent variable says nothing about whether or not there is a main effect of the other. The bottom panel of Figure 8.4 “Two Ways to Plot the Results of a Factorial Experiment With Two Independent Variables” , for example, shows a clear main effect of psychotherapy length. The longer the psychotherapy, the better it worked. But it also shows no overall advantage of one type of psychotherapy over the other.

There is an interaction effect (or just “interaction”) when the effect of one independent variable depends on the level of another. Although this might seem complicated, you have an intuitive understanding of interactions already. It probably would not surprise you, for example, to hear that the effect of receiving psychotherapy is stronger among people who are highly motivated to change than among people who are not motivated to change. This is an interaction because the effect of one independent variable (whether or not one receives psychotherapy) depends on the level of another (motivation to change). Schnall and her colleagues also demonstrated an interaction because the effect of whether the room was clean or messy on participants’ moral judgments depended on whether the participants were low or high in private body consciousness. If they were high in private body consciousness, then those in the messy room made harsher judgments. If they were low in private body consciousness, then whether the room was clean or messy did not matter.

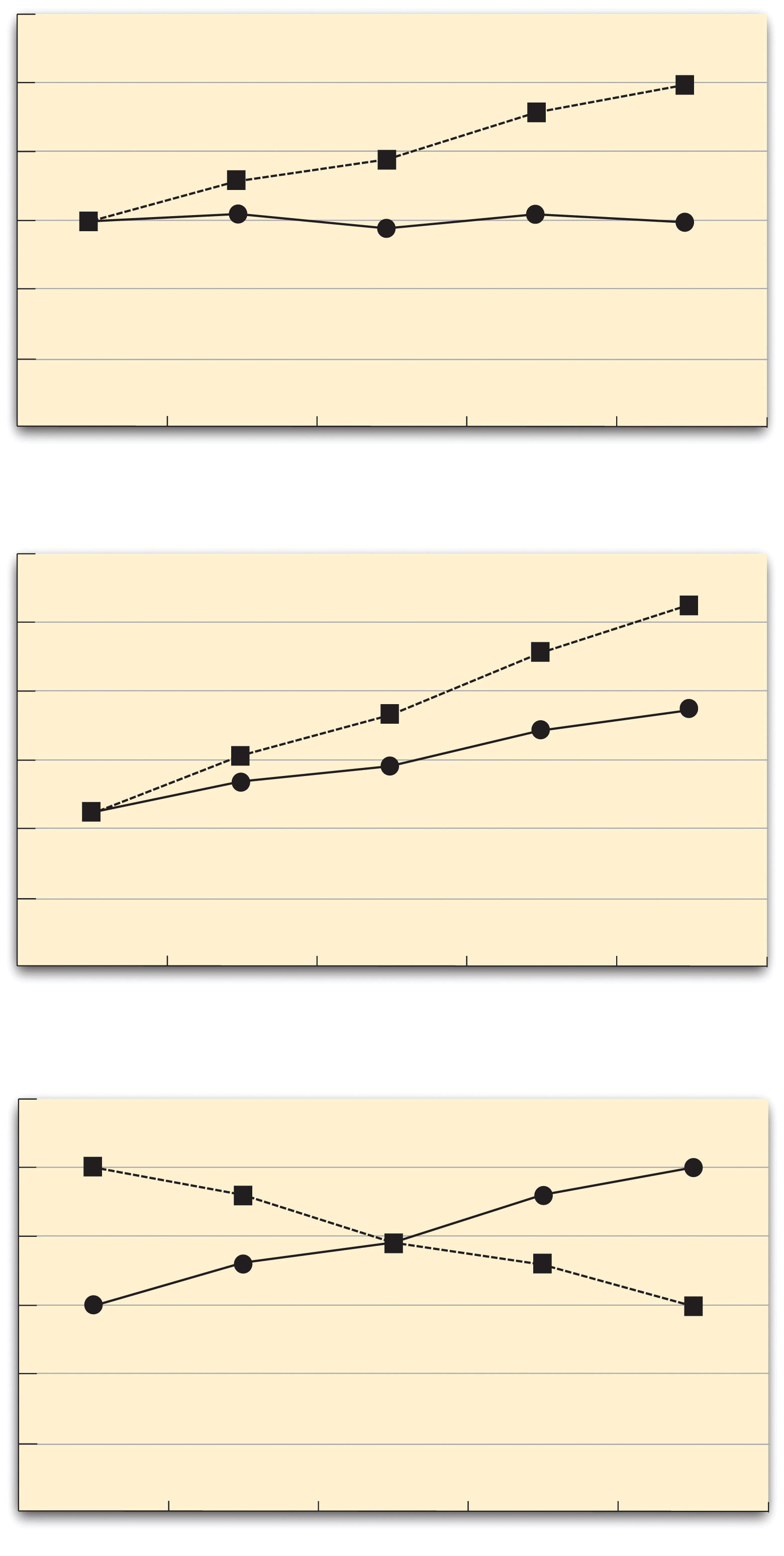
The effect of one independent variable can depend on the level of the other in different ways. This is shown in Figure 8.5 “Bar Graphs Showing Three Types of Interactions” . In the top panel, one independent variable has an effect at one level of the second independent variable but no effect at the others. (This is much like the study of Schnall and her colleagues where there was an effect of disgust for those high in private body consciousness but not for those low in private body consciousness.) In the middle panel, one independent variable has a stronger effect at one level of the second independent variable than at the other level. This is like the hypothetical driving example where there was a stronger effect of using a cell phone at night than during the day. In the bottom panel, one independent variable again has an effect at both levels of the second independent variable, but the effects are in opposite directions. Figure 8.5 “Bar Graphs Showing Three Types of Interactions” shows the strongest form of this kind of interaction, called a crossover interaction . One example of a crossover interaction comes from a study by Kathy Gilliland on the effect of caffeine on the verbal test scores of introverts and extroverts (Gilliland, 1980). Introverts perform better than extroverts when they have not ingested any caffeine. But extroverts perform better than introverts when they have ingested 4 mg of caffeine per kilogram of body weight. Figure 8.6 “Line Graphs Showing Three Types of Interactions” shows examples of these same kinds of interactions when one of the independent variables is quantitative and the results are plotted in a line graph. Note that in a crossover interaction, the two lines literally “cross over” each other.

Figure 8.5 Bar Graphs Showing Three Types of Interactions

In the top panel, one independent variable has an effect at one level of the second independent variable but not at the other. In the middle panel, one independent variable has a stronger effect at one level of the second independent variable than at the other. In the bottom panel, one independent variable has the opposite effect at one level of the second independent variable than at the other.

Figure 8.6 Line Graphs Showing Three Types of Interactions

In many studies, the primary research question is about an interaction. The study by Brown and her colleagues was inspired by the idea that people with hypochondriasis are especially attentive to any negative health-related information. This led to the hypothesis that people high in hypochondriasis would recall negative health-related words more accurately than people low in hypochondriasis but recall non-health-related words about the same as people low in hypochondriasis. And of course this is exactly what happened in this study.

Key Takeaways

• Researchers often include multiple independent variables in their experiments. The most common approach is the factorial design, in which each level of one independent variable is combined with each level of the others to create all possible conditions.
• In a factorial design, the main effect of an independent variable is its overall effect averaged across all other independent variables. There is one main effect for each independent variable.
• There is an interaction between two independent variables when the effect of one depends on the level of the other. Some of the most interesting research questions and results in psychology are specifically about interactions.
• Practice: Return to the five article titles presented at the beginning of this section. For each one, identify the independent variables and the dependent variable.
• Practice: Create a factorial design table for an experiment on the effects of room temperature and noise level on performance on the SAT. Be sure to indicate whether each independent variable will be manipulated between subjects or within subjects and explain why.

Brown, H. D., Kosslyn, S. M., Delamater, B., Fama, A., & Barsky, A. J. (1999). Perceptual and memory biases for health-related information in hypochondriacal individuals. Journal of Psychosomatic Research , 47 , 67–78.

Gilliland, K. (1980). The interactive effect of introversion-extroversion with caffeine induced arousal on verbal performance. Journal of Research in Personality , 14 , 482–492.

Research Methods in Psychology Copyright © 2016 by University of Minnesota is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

15 Independent and Dependent Variable Examples

Dave Cornell (PhD)

Dr. Cornell has worked in education for more than 20 years. His work has involved designing teacher certification for Trinity College in London and in-service training for state governments in the United States. He has trained kindergarten teachers in 8 countries and helped businessmen and women open baby centers and kindergartens in 3 countries.

Learn about our Editorial Process

Chris Drew (PhD)

This article was peer-reviewed and edited by Chris Drew (PhD). The review process on Helpful Professor involves having a PhD level expert fact check, edit, and contribute to articles. Reviewers ensure all content reflects expert academic consensus and is backed up with reference to academic studies. Dr. Drew has published over 20 academic articles in scholarly journals. He is the former editor of the Journal of Learning Development in Higher Education and holds a PhD in Education from ACU.

An independent variable (IV) is what is manipulated in a scientific experiment to determine its effect on the dependent variable (DV).

By varying the level of the independent variable and observing associated changes in the dependent variable, a researcher can conclude whether the independent variable affects the dependent variable or not.

This can provide very valuable information when studying just about any subject.

Because the researcher controls the level of the independent variable, it can be determined if the independent variable has a causal effect on the dependent variable.

The term causation is vitally important. Scientists want to know what causes changes in the dependent variable. The only way to do that is to manipulate the independent variable and observe any changes in the dependent variable.

Definition of Independent and Dependent Variables

The independent variable and dependent variable are used in a very specific type of scientific study called the experiment .

Although there are many variations of the experiment, generally speaking, it involves either the presence or absence of the independent variable and the observation of what happens to the dependent variable.

The research participants are randomly assigned to either receive the independent variable (called the treatment condition), or not receive the independent variable (called the control condition).

Other variations of an experiment might include having multiple levels of the independent variable.

If the independent variable affects the dependent variable, then it should be possible to observe changes in the dependent variable based on the presence or absence of the independent variable.  

Of course, there are a lot of issues to consider when conducting an experiment, but these are the basic principles.

These concepts should not be confused with predictor and outcome variables .

Examples of Independent and Dependent Variables

1. gatorade and improved athletic performance.

A sports medicine researcher has been hired by Gatorade to test the effects of its sports drink on athletic performance. The company wants to claim that when an athlete drinks Gatorade, their performance will improve.

If they can back up that claim with hard scientific data, that would be great for sales.

So, the researcher goes to a nearby university and randomly selects both male and female athletes from several sports: track and field, volleyball, basketball, and football. Each athlete will run on a treadmill for one hour while their heart rate is tracked.

All of the athletes are given the exact same amount of liquid to consume 30-minutes before and during their run. Half are given Gatorade, and the other half are given water, but no one knows what they are given because both liquids have been colored.

In this example, the independent variable is Gatorade, and the dependent variable is heart rate.  

2. Chemotherapy and Cancer

A hospital is investigating the effectiveness of a new type of chemotherapy on cancer. The researchers identified 120 patients with relatively similar types of cancerous tumors in both size and stage of progression.

The patients are randomly assigned to one of three groups: one group receives no chemotherapy, one group receives a low dose of chemotherapy, and one group receives a high dose of chemotherapy.

Each group receives chemotherapy treatment three times a week for two months, except for the no-treatment group. At the end of two months, the doctors measure the size of each patient’s tumor.

In this study, despite the ethical issues (remember this is just a hypothetical example), the independent variable is chemotherapy, and the dependent variable is tumor size.

3. Interior Design Color and Eating Rate

A well-known fast-food corporation wants to know if the color of the interior of their restaurants will affect how fast people eat. Of course, they would prefer that consumers enter and exit quickly to increase sales volume and profit.

So, they rent space in a large shopping mall and create three different simulated restaurant interiors of different colors. One room is painted mostly white with red trim and seats; one room is painted mostly white with blue trim and seats; and one room is painted mostly white with off-white trim and seats.

Next, they randomly select shoppers on Saturdays and Sundays to eat for free in one of the three rooms. Each shopper is given a box of the same food and drink items and sent to one of the rooms. The researchers record how much time elapses from the moment they enter the room to the moment they leave.

The independent variable is the color of the room, and the dependent variable is the amount of time spent in the room eating.

4. Hair Color and Attraction

A large multinational cosmetics company wants to know if the color of a woman’s hair affects the level of perceived attractiveness in males. So, they use Photoshop to manipulate the same image of a female by altering the color of her hair: blonde, brunette, red, and brown.

Next, they randomly select university males to enter their testing facilities. Each participant sits in front of a computer screen and responds to questions on a survey. At the end of the survey, the screen shows one of the photos of the female.

At the same time, software on the computer that utilizes the computer’s camera is measuring each male’s pupil dilation. The researchers believe that larger dilation indicates greater perceived attractiveness.

The independent variable is hair color, and the dependent variable is pupil dilation.

5. Mozart and Math

After many claims that listening to Mozart will make you smarter, a group of education specialists decides to put it to the test. So, first, they go to a nearby school in a middle-class neighborhood.

During the first three months of the academic year, they randomly select some 5th-grade classrooms to listen to Mozart during their lessons and exams. Other 5 th grade classrooms will not listen to any music during their lessons and exams.

The researchers then compare the scores of the exams between the two groups of classrooms.

Although there are a lot of obvious limitations to this hypothetical, it is the first step.

The independent variable is Mozart, and the dependent variable is exam scores.

6. Essential Oils and Sleep

A company that specializes in essential oils wants to examine the effects of lavender on sleep quality. They hire a sleep research lab to conduct the study. The researchers at the lab have their usual test volunteers sleep in individual rooms every night for one week.

The conditions of each room are all exactly the same, except that half of the rooms have lavender released into the rooms and half do not. While the study participants are sleeping, their heart rates and amount of time spent in deep sleep are recorded with high-tech equipment.

At the end of the study, the researchers compare the total amount of time spent in deep sleep of the lavender-room participants with the no lavender-room participants.

The independent variable in this sleep study is lavender, and the dependent variable is the total amount of time spent in deep sleep.

7. Teaching Style and Learning

A group of teachers is interested in which teaching method will work best for developing critical thinking skills.

So, they train a group of teachers in three different teaching styles : teacher-centered, where the teacher tells the students all about critical thinking; student-centered, where the students practice critical thinking and receive teacher feedback; and AI-assisted teaching, where the teacher uses a special software program to teach critical thinking.

At the end of three months, all the students take the same test that assesses critical thinking skills. The teachers then compare the scores of each of the three groups of students.

The independent variable is the teaching method, and the dependent variable is performance on the critical thinking test.

8. Concrete Mix and Bridge Strength

A chemicals company has developed three different versions of their concrete mix. Each version contains a different blend of specially developed chemicals. The company wants to know which version is the strongest.

So, they create three bridge molds that are identical in every way. They fill each mold with one of the different concrete mixtures. Next, they test the strength of each bridge by placing progressively more weight on its center until the bridge collapses.

In this study, the independent variable is the concrete mixture, and the dependent variable is the amount of weight at collapse.

9. Recipe and Consumer Preferences

People in the pizza business know that the crust is key. Many companies, large and small, will keep their recipe a top secret. Before rolling out a new type of crust, the company decides to conduct some research on consumer preferences.

The company has prepared three versions of their crust that vary in crunchiness, they are: a little crunchy, very crunchy, and super crunchy. They already have a pool of consumers that fit their customer profile and they often use them for testing.

Each participant sits in a booth and takes a bite of one version of the crust. They then indicate how much they liked it by pressing one of 5 buttons: didn’t like at all, liked, somewhat liked, liked very much, loved it.

The independent variable is the level of crust crunchiness, and the dependent variable is how much it was liked.

10. Protein Supplements and Muscle Mass

A large food company is considering entering the health and nutrition sector. Their R&D food scientists have developed a protein supplement that is designed to help build muscle mass for people that work out regularly.

The company approaches several gyms near its headquarters. They enlist the cooperation of over 120 gym rats that work out 5 days a week. Their muscle mass is measured, and only those with a lower level are selected for the study, leaving a total of 80 study participants.

They randomly assign half of the participants to take the recommended dosage of their supplement every day for three months after each workout. The other half takes the same amount of something that looks the same but actually does nothing to the body.

At the end of three months, the muscle mass of all participants is measured.

The independent variable is the supplement, and the dependent variable is muscle mass.  

11. Air Bags and Skull Fractures

In the early days of airbags , automobile companies conducted a great deal of testing. At first, many people in the industry didn’t think airbags would be effective at all. Fortunately, there was a way to test this theory objectively.

In a representative example: Several crash cars were outfitted with an airbag, and an equal number were not. All crash cars were of the same make, year, and model. Then the crash experts rammed each car into a crash wall at the same speed. Sensors on the crash dummy skulls allowed for a scientific analysis of how much damage a human skull would incur.

The amount of skull damage of dummies in cars with airbags was then compared with those without airbags.

The independent variable was the airbag and the dependent variable was the amount of skull damage.

12. Vitamins and Health

Some people take vitamins every day. A group of health scientists decides to conduct a study to determine if taking vitamins improves health.

They randomly select 1,000 people that are relatively similar in terms of their physical health. The key word here is “similar.”

Because the scientists have an unlimited budget (and because this is a hypothetical example, all of the participants have the same meals delivered to their homes (breakfast, lunch, and dinner), every day for one year.

In addition, the scientists randomly assign half of the participants to take a set of vitamins, supplied by the researchers every day for 1 year. The other half do not take the vitamins.

At the end of one year, the health of all participants is assessed, using blood pressure and cholesterol level as the key measurements.

In this highly unrealistic study, the independent variable is vitamins, and the dependent variable is health, as measured by blood pressure and cholesterol levels.

13. Meditation and Stress

Does practicing meditation reduce stress? If you have ever wondered if this is true or not, then you are in luck because there is a way to know one way or the other.

All we have to do is find 90 people that are similar in age, stress levels, diet and exercise, and as many other factors as we can think of.

Next, we randomly assign each person to either practice meditation every day, three days a week, or not at all. After three months, we measure the stress levels of each person and compare the groups.

How should we measure stress? Well, there are a lot of ways. We could measure blood pressure, or the amount of the stress hormone cortisol in their blood, or by using a paper and pencil measure such as a questionnaire that asks them how much stress they feel.

In this study, the independent variable is meditation and the dependent variable is the amount of stress (however it is measured).

14. Video Games and Aggression

When video games started to become increasingly graphic, it was a huge concern in many countries in the world. Educators, social scientists, and parents were shocked at how graphic games were becoming.

Since then, there have been hundreds of studies conducted by psychologists and other researchers. A lot of those studies used an experimental design that involved males of various ages randomly assigned to play a graphic or non-graphic video game.

Afterward, their level of aggression was measured via a wide range of methods, including direct observations of their behavior, their actions when given the opportunity to be aggressive, or a variety of other measures.

So many studies have used so many different ways of measuring aggression.

In these experimental studies, the independent variable was graphic video games, and the dependent variable was observed level of aggression.

15. Vehicle Exhaust and Cognitive Performance

Car pollution is a concern for a lot of reasons. In addition to being bad for the environment, car exhaust may cause damage to the brain and impair cognitive performance.

One way to examine this possibility would be to conduct an animal study. The research would look something like this: laboratory rats would be raised in three different rooms that varied in the degree of car exhaust circulating in the room: no exhaust, little exhaust, or a lot of exhaust.

After a certain period of time, perhaps several months, the effects on cognitive performance could be measured.

One common way of assessing cognitive performance in laboratory rats is by measuring the amount of time it takes to run a maze successfully. It would also be possible to examine the physical effects of car exhaust on the brain by conducting an autopsy.

In this animal study, the independent variable would be car exhaust and the dependent variable would be amount of time to run a maze.

Read Next: Extraneous Variables Examples

The experiment is an incredibly valuable way to answer scientific questions regarding the cause and effect of certain variables. By manipulating the level of an independent variable and observing corresponding changes in a dependent variable, scientists can gain an understanding of many phenomena.

For example, scientists can learn if graphic video games make people more aggressive, if mediation reduces stress, if Gatorade improves athletic performance, and even if certain medical treatments can cure cancer.

The determination of causality is the key benefit of manipulating the independent variable and them observing changes in the dependent variable. Other research methodologies can reveal factors that are related to the dependent variable or associated with the dependent variable, but only when the independent variable is controlled by the researcher can causality be determined.

Ferguson, C. J. (2010). Blazing Angels or Resident Evil? Can graphic video games be a force for good? Review of General Psychology, 14 (2), 68-81. https://doi.org/10.1037/a0018941

Flannelly, L. T., Flannelly, K. J., & Jankowski, K. R. (2014). Independent, dependent, and other variables in healthcare and chaplaincy research. Journal of Health Care Chaplaincy , 20 (4), 161–170. https://doi.org/10.1080/08854726.2014.959374

Manocha, R., Black, D., Sarris, J., & Stough, C.(2011). A randomized, controlled trial of meditation for work stress, anxiety and depressed mood in full-time workers. Evidence-Based Complementary and Alternative Medicine , vol. 2011, Article ID 960583. https://doi.org/10.1155/2011/960583

Rumrill, P. D., Jr. (2004). Non-manipulation quantitative designs. Work (Reading, Mass.) , 22 (3), 255–260.

Taylor, J. M., & Rowe, B. J. (2012). The “Mozart Effect” and the mathematical connection, Journal of College Reading and Learning, 42 (2), 51-66.  https://doi.org/10.1080/10790195.2012.10850354

• Dave Cornell (PhD) https://helpfulprofessor.com/author/dave-cornell-phd/ 23 Achieved Status Examples
• Dave Cornell (PhD) https://helpfulprofessor.com/author/dave-cornell-phd/ 25 Defense Mechanisms Examples
• Dave Cornell (PhD) https://helpfulprofessor.com/author/dave-cornell-phd/ 15 Theory of Planned Behavior Examples
• Dave Cornell (PhD) https://helpfulprofessor.com/author/dave-cornell-phd/ 18 Adaptive Behavior Examples

• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd-2/ 23 Achieved Status Examples
• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd-2/ 15 Ableism Examples
• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd-2/ 25 Defense Mechanisms Examples
• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd-2/ 15 Theory of Planned Behavior Examples

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

Design of Experiments with Multiple Independent Variables: A Resource Management Perspective on Complete and Reduced Factorial Designs

Linda m collins, john j dziak.

• Author information
• Copyright and License information

Correspondence may be sent to Linda M. Collins, The Methodology Center, Penn State, 204 E. Calder Way, Suite 400, State College, PA 16801; [email protected]

An investigator who plans to conduct experiments with multiple independent variables must decide whether to use a complete or reduced factorial design. This article advocates a resource management perspective on making this decision, in which the investigator seeks a strategic balance between service to scientific objectives and economy. Considerations in making design decisions include whether research questions are framed as main effects or simple effects; whether and which effects are aliased (confounded) in a particular design; the number of experimental conditions that must be implemented in a particular design and the number of experimental subjects the design requires to maintain the desired level of statistical power; and the costs associated with implementing experimental conditions and obtaining experimental subjects. In this article four design options are compared: complete factorial, individual experiments, single factor, and fractional factorial designs. Complete and fractional factorial designs and single factor designs are generally more economical than conducting individual experiments on each factor. Although relatively unfamiliar to behavioral scientists, fractional factorial designs merit serious consideration because of their economy and versatility.

Keywords: experimental design, fractional factorial designs, factorial designs, reduced designs, resource management

Suppose a scientist is interested in investigating the effects of k independent variables, where k > 1. For example, Bolger and Amarel (2007) investigated the hypothesis that the effect of peer social support on performance stress can be positive or negative, depending on whether the way the peer social support is given enhances or degrades self-efficacy. Their experiment could be characterized as involving four factors: support offered (yes or no), nature of support (visible or indirect), message from a confederate that recipient of support is unable to handle the task alone (yes or no), and message that a confederate would be unable to handle the task (yes or no).

One design possibility when k > 1 independent variables are to be examined is a factorial experiment. In factorial research designs, experimental conditions are formed by systematically varying the levels of two or more independent variables, or factors. For example, in the classic two × two factorial design there are two factors each with two levels. The two factors are crossed, that is, all combinations of levels of the two factors are formed, to create a design with four experimental conditions. More generally, factorial designs can include k ≥ 2 factors and can incorporate two or more levels per factor. With four two-level variables, such as in Bolger and Amarel (2007) , a complete factorial experiment would involve 2 × 2 × 2 × 2 = 16 experimental conditions. One advantage of factorial designs, as compared to simpler experiments that manipulate only a single factor at a time, is the ability to examine interactions between factors. A second advantage of factorial designs is their efficiency with respect to use of experimental subjects; factorial designs require fewer experimental subjects than comparable alternative designs to maintain the same level of statistical power (e.g. Wu & Hamada, 2000 ).

However, a complete factorial experiment is not always an option. In some cases there may be combinations of levels of the factors that would create a nonsensical, toxic, logistically impractical or otherwise undesirable experimental condition. For example, Bolger and Amarel (2007) could not have conducted a complete factorial experiment because some of the combinations of levels of the factors would have been illogical (e.g. no support offered but support was direct). But even when all combinations of factors are reasonable, resource limitations may make implementation of a complete factorial experiment impossible. As the number of factors and levels of factors under consideration increases, the number of experimental conditions that must be implemented in a complete factorial design increases rapidly. The accompanying logistical difficulty and expense may exceed available resources, prompting investigators to seek alternative experimental designs that require fewer experimental conditions.

In this article the term “reduced design” will be used to refer generally to any design approach that involves experimental manipulation of all k independent variables, but includes fewer experimental conditions than a complete factorial design with the same k variables. Reduced designs are often necessary to make simultaneous investigation of multiple independent variables feasible. However, any removal of experimental conditions to form a reduced design has important scientific consequences. The number of effects that can be estimated in an experimental design is limited to one fewer than the number of experimental conditions represented in the design. Therefore, when experimental conditions are removed from a design some effects are combined so that their sum only, not the individual effects, can be estimated. Another way to think of this is that two or more interpretational labels (e.g. main effect of Factor A; interaction between Factor A and Factor B) can be applied to the same source of variation. This phenomenon is known as aliasing (sometimes referred to as confounding, or as collinearity in the regression framework).

Any investigator who wants or needs to examine multiple independent variables is faced with deciding whether to use a complete factorial or a reduced experimental design. The best choice is one that strikes a careful and strategic balance between service to scientific objectives and economy. Weighing a variety of considerations to achieve such a balance, including the exact research questions of interest, the potential impact of aliasing on interpretation of results, and the costs associated with each design option, is the topic of this article.

Objectives of this article

This article has two objectives. The first objective is to propose that a resource management perspective may be helpful to investigators who are choosing a design for an experiment that will involve several independent variables. The resource management perspective assumes that an experiment is motivated by a finite set of research questions and that these questions can be prioritized for decision making purposes. Then according to this perspective the preferred experimental design is the one that, in relation to the resource requirements of the design, offers the greatest potential to advance the scientific agenda motivating the experiment. Four general design alternatives will be considered from a resource management perspective: complete factorial designs and three types of reduced designs. One of the reduced designs, the fractional factorial, is used routinely in engineering but currently unfamiliar to many social and behavioral scientists. In our view fractional factorial designs merit consideration by social and behavioral scientists alongside other more commonly used reduced designs. Accordingly, a second objective of this article is to offer a brief introductory tutorial on fractional factorial designs, in the hope of assisting investigators who wish to evaluate whether these designs might be of use in their research.

Overview of four design alternatives

Throughout this article, it is assumed that an investigator is interested in examining the effects of k independent variables, each of which could correspond to a factor in a factorial experiment. It is not necessarily a foregone conclusion that the k independent variables must be examined in a single experiment; they may represent a set of questions comprising a program of research, or a set of features or components comprising a behavioral intervention program. It is assumed that the k factors can be independently manipulated, and that no possible combination of the factors would create an experimental condition that cannot or should not be implemented. For the sake of simplicity, it is also assumed that each of the k factors has only two levels, such as On/Off or Yes/No. Factorial and fractional factorial designs can be done with factors having any number of levels, but two-level factors allow the most straightforward interpretation and largest statistical power, especially for interactions.

In this section the four different design alternatives considered in this article are introduced using a hypothetical example based on the following scenario: An investigator is to conduct a study on anxiety related to public speaking (this example is modeled very loosely on Bolger and Amarel, 2007 ). There are three factors of theoretical interest to the investigator, each with two levels, On or Off. The factors are whether or not (1) the subject is allowed to choose a topic for the presentation ( choose ); (2) the subject is taught a deep-breathing relaxation exercise to perform just before giving the presentation ( breath ); and (3) the subject is provided with extra time to prepare for the speech ( prep ). This small hypothetical example will be useful in illustrating some initial key points of comparison among the design alternatives. Later in the article the hypothetical example will be extended to include more factors so that some additional points can be illustrated.

The first alternative considered here is a complete factorial design. The remaining alternatives considered are reduced designs, each of which can be viewed as a subset of the complete factorial.

Complete factorial designs

Factorial designs may be denoted using the exponential notation 2 k , which compactly expresses that k factors with 2 levels each are crossed, resulting in 2 k experimental conditions (sometimes called “cells”). Each experimental condition represents a unique combination of levels of the k factors. In the hypothetical example a complete factorial design would be expressed as 2 3 (or equivalently, 2 × 2 × 2) and would involve eight experimental conditions. Table 1 shows these eight experimental conditions along with effect coding. The design enables estimation of seven effects: three main effects, three two-way interactions, and a single three-way interaction.

Table 1. Effect Coding for Complete Factorial Design with Three 2-Level Factors.

Table 1 illustrates one feature of complete factorial designs in which an equal number of subjects is assigned to each experimental condition, namely the balance property. A design is balanced if each level of each factor appears in the design the same number of times and is assigned to the same number of subjects ( Hays, 1994 ; Wu & Hamada, 2000 ). In a balanced design the main effects and interactions are orthogonal, so that each one is estimated and tested as if it were the only one under consideration, with very little loss of efficiency due to the presence of other factors 1 . (Effects may still be orthogonal even in unbalanced designs if certain proportionality conditions are met; see e.g. Hays, 1994 , p. 475.) The balance property is evident in Table 1 ; each level of each factor appears exactly four times.

Individual experiments

The individual experiments approach requires conducting a two-condition experiment for each independent variable, that is, k separate experiments. In the example this would require conducting three different experiments, involving a total of six experimental conditions. In one experiment, a condition in which subjects are allowed to choose the topic of the presentation would be compared to one in which subjects are assigned a topic; in a second experiment, a condition in which subjects are taught a relaxation exercise would be compared to one in which no relaxation exercise is taught; in a third experiment, a condition in which subjects are given ample time to prepare in advance would be compared to one in which subjects are given little preparation time. The subset of experimental conditions from the complete three-factor factorial experiment in Table 1 that would be implemented in the individual experiments approach is depicted in the first section of Table 2 . This design, considered as a whole, is not balanced. Each of the independent variables is set to On once and set to Off five times.

Table 2. Effect Coding for Reduced Designs That Comprise Subsets of the Design in Table 1 .

Single factor designs in which the factor has many levels.

In the single factor approach a single experiment is performed in which various combinations of levels of the independent variables are selected to form one nominal or ordinal categorical factor with several qualitatively distinct levels. West, Aiken, and Todd (1993 ; West & Aiken, 1997 ) reviewed three variations of the single factor design that are used frequently, particularly in research on behavioral interventions for prevention and treatment. In the comparative treatment design there are k +1 experimental conditions: k experimental conditions in which one independent variable is set to On and all the others to Off, plus a single control condition in which all independent variables are set to Off. This approach is similar to conducting separate individual experiments, except that a shared control group is used for all factors. The second section of Table 2 shows the four experimental conditions that would comprise a comparative treatment design in the hypothetical example. These are the same experimental conditions that appear in the individual experiments design.

By contrast, for the constructive treatment design an intervention is “built” by combining successive features. For example, an investigator interested in developing a treatment to reduce anxiety might want to assess the effect of allowing the subject to choose a topic, then the incremental effect of also teaching a relaxation exercise, then the incremental effect of allowing extra preparation time. The third section of Table 2 shows the subset of experimental conditions from the complete factorial shown in Table 1 that would be implemented in a three-factor constructive treatment experiment in which first choose is added, followed by breath and then prep . The constructive treatment strategy typically has k +1 experimental conditions but may have fewer or more. The dismantling design, in which the objective is to determine the effect of removing one or more features of an intervention, and other single factor designs are based on similar logic.

Table 2 shows that both the comparative treatment design and the constructive treatment design are unbalanced. In the comparative treatment design, each factor is set to On once and set to Off three times. In the constructive treatment design, choose is set to Off once and to On three times, and prep is set to On once and to Off three times. Other single factor designs are similarly unbalanced.

Fractional factorial designs

The fourth alternative considered in this article is to use a design from the family of fractional factorial designs. A fractional factorial design involves a special, carefully chosen subset, or fraction, of the experimental conditions in a complete factorial design. The bottom section of Table 2 shows a subset of experimental conditions from the complete three-factor factorial design that constitute a fractional factorial design. The experimental conditions in fractional factorial designs are selected so as to preserve the balance property. 2 As Table 2 shows, each level of each factor appears in the design exactly twice.

Fractional factorial designs are represented using an exponential notation based on that used for complete factorial designs. The fractional factorial design in Table 2 would be expressed as 2 3−1 . This notation contains the following information: (a) the corresponding complete factorial design is 2 3 , in other words involves 3 factors, each of which has 2 levels, for a total of 8 experimental conditions; (b) the fractional factorial design involves 2 3−1 = 2 2 = 4 experimental conditions; and (c) this fractional factorial design is a 2 −1 = 1/2 fraction of the complete factorial. Many fractional factorial designs, particularly those with many factors, involve even smaller fractions of the complete factorial.

Aliasing in the individual experiments, single factor, and fractional factorial designs

It was mentioned above that reduced designs involve aliasing of effects. A design's aliasing is evident in its effect coding. When effects are aliased their effect coding is perfectly correlated (whether positively or negatively). Aliasing in the individual experiments approach can be seen by examining the first section of Table 2 . In the experiment examining choose , the effect codes are identical for the main effect of choose and the choose × breath × prep interaction (−1 for experimental condition 1 and 1 for experimental condition 4), and these are perfectly negatively correlated with the effect codes for the choose × breath and choose × prep interactions. Thus these effects are aliased; the effect estimated by this experiment is an aggregate of the main effect of choose and all of the interactions involving choose . (The codes for the remaining effects, namely the main effects of breath and prep and the breath × prep interaction, are constants in this design.) Similarly, in the experiment investigating breath , the main effect and all of the interactions involving breath are aliased, and in the experiment investigating prep , the main effect and all of the interactions involving prep are aliased.

The aliasing in single factor experiments using the comparative treatment strategy is identical to the aliasing in the individual experiments approach. As shown in the second section of Table 2 , for the hypothetical example a comparative treatment experiment would involve experimental conditions 1, 2, 3, and 5, which are the same conditions as in the individual experiments approach. The effects of each factor are assessed by means of the same comparisons; for example, the effect of choose would be assessed by comparing experimental conditions 1 and 5. The primary difference is that only one control condition would be required in the single factor experiment, whereas in the individual experiments approach three control conditions are required.

The constructive treatment strategy is comprised of a different subset of experimental conditions from the full factorial than the individual experiments and comparative treatment approaches. Nevertheless, the aliasing is similar. As the third section of Table 2 shows, the effect of adding choose would be assessed by comparing experimental conditions 1 and 5, so the aliasing would be the same as that in the individual experiment investigating choose discussed above. The cumulative effect of adding breath would be assessed by comparing experimental conditions 5 and 7. The effect codes in these two experimental conditions for the main effect of breath are perfectly (positively or negatively) correlated with those for all of the interactions involving breath , although here the effect codes for the interactions are reversed as compared to the individual experiments and comparative treatment approaches. The same reasoning applies to the effect of prep , which is assessed by comparing experimental conditions 7 and 8.

As the fourth section of Table 2 illustrates, the aliasing in fractional factorial designs is different from the aliasing seen in the individual experiments and single factor approaches. In this fractional factorial design the effect of choose is estimated by comparing the mean of experimental conditions 2 and 3 with the mean of experimental conditions 5 and 8; the effect of breath is estimated by comparing the mean of experimental conditions 3 and 8 to the mean of experimental conditions 2 and 5; and the effect of prep is estimated by comparing the mean of experimental conditions 2 and 8 to the mean of experimental conditions 3 and 5. The effect codes show that the main effect of choose and the breath × prep interaction are aliased. The remaining effects are either orthogonal to the aliased effect or constant. Similarly, the main effect of breath and the choose × prep interaction are aliased, and the main effect of prep and the choose × breath interaction are aliased.

Note that each source of variation in this fractional factorial design has two aliases (e.g. choose and the breath × prep interaction form a single source of variation). This is characteristic of fractional factorial designs that, like this one, are 1/2 fractions. The denominator of the fraction always reveals how many aliases each source of variation has. Thus in a fractional factorial design that is a 1/4 fraction each source of variation has four aliases; in a fractional factorial design that is a 1/8 fraction each source of variation has eight aliases; and so on.

Aliasing and scientific questions

An investigator who is interested in using a reduced design to estimate the effects of k factors faces several considerations. These include: whether the research questions of primary scientific interest concern simple effects or main effects; whether the design's aliasing means that assumptions must be made in order to address the research questions; and how to use aliasing strategically. Each of these considerations is reviewed in this section.

Simple effects and main effects

In this article we have been discussing a situation in which a finite set of k independent variables is under consideration and the individual effects of each of the k variables are of interest. However, the question “Does a particular factor have an effect?” is incomplete; different research questions may involve different types of effects. Let us examine three different research questions concerning the effect of breath in the hypothetical example, and see how they correspond to effects in a factorial design.

Question 1: “Does the factor breath have an effect on the outcome variable when the factors choose and prep are set to Off?”

Question 2: “Will an intervention consisting of only the factors choose and prep set to On be improved if the factor breath is changed from Off to On?”

Question 3: “Does the factor breath have an effect on the outcome variable on average across levels of the other factors?”

In the language of experimental design, Questions 1 and 2 concern simple effects, and Question 3 concerns a main effect. The distinction between simple effects and main effects is subtle but important. A simple effect of a factor is an effect at a particular combination of levels of the remaining factors. There are as many simple effects for each factor as there are combinations of levels of the remaining factors. For example, the simple effect relevant to Question 1 is the conditional effect of changing breath from Off to On, assuming both prep and choose are set to Off. The simple effect relevant to Question 2 is the conditional effect of changing breath from Off to On, assuming both other factors are set to On. Thus although Questions 1 and 2 both are concerned with simple effects of breath , they are concerned with different simple effects.

A significant main effect for a factor is an effect on average across all combinations of levels of the other factors in the experiment. For example, Question 3 is concerned with the main effect of breath , that is, the effect of breath averaged across all combinations of levels of prep and choose . Given a particular set of k factors, there is only one main effect corresponding to each factor.

Simple effects and main effects are not interchangeable, unless we assume that all interactions are negligible. Thus, neither necessarily tells anything about the other. A positive main effect does not imply that all of the simple effects are nonzero or even nonnegative. It is even possible (due to a large interaction) for one simple effect to be positive, another simple effect for the same factor to be negative, and the main (averaged) effect to be zero. In the public speaking example, the answer to Question 2 does not imply anything about whether an intervention consisting of breath alone would be effective, or whether there would be an incremental effect of breath if it were added to an intervention initially consisting of choose alone.

Research questions, aliasing, and assumptions

Suppose an investigator is interested in addressing Question 1 above. The answer to this research question depends only upon the particular simple effect of breath when both of the other factors are set to Off. The research question does not ask whether any observed differences are attributable to the main effect of breath , the breath × prep interaction, the breath × choose interaction, the breath × prep × choose interaction, or some combination of the aliased effects. The answer to Question 2, which also concerns a simple effect, depends only upon whether changing breath from Off to On has an effect on the outcome variable when prep and choose are set to On; it does not depend on establishing whether any other effects in the model are present or absent. As Kirk (1968) pointed out, simple effects “represent a partition of a treatment sum of squares plus an interaction sum of squares” (p. 380). Thus, although there is aliasing in the individual experiments and comparative treatment strategies, these designs are appropriate for addressing Question 1, because the aliased effects correspond exactly to the effect of interest in Question 1. Similarly, although there is aliasing in the constructive treatment strategy, this design is appropriate for addressing Question 2. In other words, although in our view it is important to be aware of aliasing whenever considering a reduced experimental design, the aliasing ultimately is of little consequence if the aliased effect as a package is of primary scientific interest.

The individual experiments and comparative treatment strategies would not be appropriate for addressing Question 2. The constructive treatment strategy could address Question 1, but only if breath was the first factor set high, with the others low, in the first non-control group. The conclusions drawn from these experiments would be limited to simple effects and cannot be extended to main effects or interactions.

The situation is different if a reduced design is to be used to estimate main effects. Suppose an investigator is interested in addressing Question 3, that is, is interested in the main effect of breath . As was discussed above, in the individual experiments, comparative treatment, and constructive treatment approaches the main effect of breath is aliased with all the interactions involving breath . It is appropriate to use these designs to draw conclusions about the main effect of breath only if it is reasonable to assume that all of the interactions involving breath up to the k -way interaction are negligible. Then any effect of breath observed using an individual experiment or a single factor design is attributable to the main effect.

The difference in the aliasing structure of fractional factorial designs as compared to individual experiments and single factor designs becomes particularly salient when the primary scientific questions that motivate an experiment require estimating main effects as opposed to simple effects, and when larger numbers of factors are involved. However, the small three-factor fractional factorial experiment in Table 2 can be used to demonstrate the logic behind the choice of a particular fractional factorial design. In the design in Table 2 the main effect of breath is aliased with one two-way interaction: prep × choose . If it is reasonable to assume that this two-way interaction is negligible, then it is appropriate to use this fractional factorial design to estimate the main effect of breath . In general, investigators considering using a fractional factorial design seek a design in which main effects and scientifically important interactions are aliased only with effects that can be assumed to be negligible.

Many fractional factorial designs in which there are four or more factors require many fewer and much weaker assumptions for estimation of main effects than those required by the small hypothetical example used here. For these larger problems it is possible to identify a fractional factorial design that uses fewer experimental conditions than the complete design but in which main effects and also two-way interaction are aliased only with interactions involving three or more factors. Many of these designs also enable identification of some three-way interactions that are to be aliased only with interactions involving four or more factors. In general, the appeal of fractional factorial designs increases as the number of factors becomes larger. By contrast, individual experiments and single factor designs always alias main effects and all interactions from the two-way up to the k -way, no matter how many factors are involved.

Strategic aliasing and designating negligible effects

A useful starting point for choosing a reduced design is sorting all of the effects in the complete factorial into three categories: (1) effects that are of primary scientific interest and therefore are to be estimated; (2) effects that are expected to be zero or negligible; and (3) effects that are not of primary scientific interest but may be non-negligible. Strategic aliasing involves ensuring that effects of primary scientific interest are aliased only with negligible effects. There may be non-negligible effects that are not of scientific interest. Resources are not to be devoted to estimating such effects, but care must be taken not to alias them with effects of primary scientific interest.

Considering which, if any, effects to place in the negligible category is likely to be an unfamiliar, and perhaps in some instances uncomfortable, process for some social and behavioral scientists. However, the choice is critically important. On the one hand, when more effects are designated negligible the available options will in general include designs involving smaller numbers of experimental conditions; on the other hand, incorrectly designating effects as negligible can threaten the validity of scientific conclusions. The best bases for making assumptions about negligible effects are theory and prior empirical research. Yet there are few areas in the social and behavioral sciences in which theory makes specific predictions about higher-order interactions, and it appears that to date there has been relatively little empirical investigation of such interactions. Given this lack of guidance, on what basis can an investigator decide on assumptions?

A very cautious approach would be to assume that each and every interaction up to the k -way interaction is likely to be sizeable, unless there is empirical evidence or a compelling theoretical basis for assuming that it is negligible. This is equivalent to leaving the negligible category empty and designating each effect either of primary scientific interest or non-negligible. There are two strategies consistent with this perspective. One is to conduct a complete factorial experiment, being careful to ensure adequate statistical power to detect any interactions of scientific interest. The other strategy consistent with assuming all interactions are likely to be sizeable is to frame research questions only about simple effects that can reasonably be estimated with the individual experiments or single factor approaches. For example, as discussed above the aliasing associated with the comparative treatment design may not be an issue if research questions are framed in terms of simple effects.

If these cautious strategies seem too restrictive, another possibility is to adopt some heuristic guiding principles (see Wu & Hamada, 2000 ) that are used in engineering research for informing the choice of assumptions and aliasing structure and to help target resources in areas where they are likely to result in the most scientific progress. The guiding principles are intended for use when theory and prior research are unavailable; if guidance from these sources is available it should always be applied first. One guiding principle is called Hierarchical Ordering . This principle states that when resources are limited, the first priority should be estimation of lower order effects. Thus main effects are the first investigative priority, followed by two-way interactions. As Green and Rao (1971) noted, “…in many instances the simpler (additive) model represents a very good approximation of reality” (p. 359), particularly if measurement quality is good and floor and ceiling effects can be avoided. Another guiding principle is called Effect Sparsity ( Box & Meyer, 1986 ), or sometimes the Pareto Principle in Experimental Design ( Wu & Hamada, 2000 ). This principle states that the number of sizeable and important effects in a factorial experiment is small in comparison to the overall number of effects. Taken together, these principles suggest that unless theory and prior research specifically suggest otherwise, there are likely to be relatively few sizeable interactions except for a few two-way interactions and even fewer three-way interactions, and that aliasing the more complex and less interpretable higher-order interactions may well be a good choice.

Resolution of fractional factorial designs

Some general information about aliasing of main effects and two-way interactions is conveyed in a fractional factorial design's resolution ( Wu & Hamada, 2000 ). Resolution is designated by a Roman numeral, usually either III, IV, V or VI. The aliasing of main effects and two-way interactions in these designs is shown in Table 3 . As Table 3 shows, as design resolution increases main effects and two-way interactions become increasingly free of aliasing with lower-order interactions. Importantly, no design that is Resolution III or higher aliases main effects with other main effects.

Table 3. Resolution of Fractional Factorial Designs and Aliasing of Effects.

Table 3 shows only which effects are not aliased with main effects and two-way interactions. Which and how many effects are aliased with main effects and two-way interactions depends on the exact design. For example, consider a 2 6−2 fractional factorial design. As mentioned previously, this is a 1/4 fraction design, so each source of variance has four aliases; thus each main effect is aliased with three other effects. Suppose this design is Resolution IV. Then none of the three effects aliased with the main effect will be another main effect or a two-way interaction. Instead, they will be three higher-order interactions.

According to the Hierarchical Ordering and Effect Sparsity principles, in the absence of theory or evidence to the contrary it is reasonable to make the working assumption that higher-order interactions are less likely to be sizeable than lower-order interactions. Thus, all else being equal, higher resolution designs, which alias scientifically important main effects and two-way interactions with higher-order interactions, are preferred to lower resolution designs, which alias these effects with lower-order interactions or with main effects. This concept has been called the maximum resolution criterion by Box and Hunter (1961) .

In general higher resolution designs tend to require more experimental conditions, although for a given number of experimental conditions there may be design alternatives with different resolutions.

Relative resource requirements of the four design alternatives

Number of experimental conditions and subjects required.

The four design options considered here can vary widely with respect to the number of experimental conditions that must be implemented and the number of subjects required to achieve a given statistical power. These two resource requirements must be considered separately. In single factor experiments, the number of subjects required to perform the experiment is directly proportional to the number of experimental conditions to be implemented. However, when comparing different designs in a multi-factor framework this is not the case. For instance, a complete factorial may require many more experimental conditions than the corresponding individual experiments or single factor approach, yet require fewer total subjects.

Table 4 shows how to compute a comparison of the number of experimental conditions required by each of the four design alternatives. As Table 4 indicates, the individual experiments, single factor and fractional factorial approaches are more economical than the complete factorial approach in terms of number of experimental conditions that must be implemented. In general, the single factor approach requires the fewest experimental conditions.

Table 4. Aliasing and Economy of Four Design Approaches with k 2-level Independent Variables.

N = total sample size required to maintain desired level of power in complete factorial design.

Table 4 also provides a comparison of the minimum number of subjects required to maintain the same level of statistical power. Suppose a total of k factors are to be investigated, with the smallest effect size among them equal to d , and that a total minimum sample size of N is required in order to maintain a desired level of statistical power at a particular Type I error rate. The effect size d might be the expected normalized difference between two means, or it might be the smallest normalized difference considered clinically or practically significant. (Note that in practice there must be at least one subject per experimental condition, so at a minimum N must at least equal the number of experimental conditions. This may require additional subjects beyond the number needed to achieve a given level of power when implementing complete factorial designs with large k .) Table 4 shows that the complete factorial and fractional factorial designs are most economical in terms of sample size requirements. In any balanced factorial design each main effect is estimated using all subjects, averaging across the other main effects. In the hypothetical three-factor example, the main effects of choose , breath and prep are each based on all N subjects, with the subjects sorted differently into treatment and control groups for each main effect estimate. For example, Table 2 shows that in both the complete and fractional factorial designs a subject assigned to experimental condition 3 is in the Off group for the purpose of estimating the main effects of choose and prep but in the On group for the purpose of estimating the main effect of breath .

Essentially factorial designs “recycle” subjects by placing every subject in one of the levels of every factor. As long as the sample sizes in each group are balanced, orthogonality is maintained, so that estimation and testing for each effect can be treated as independent of the other effects. (The idea of “balance” here assumes that each level of each factor is assigned exactly the same amount of subjects, which may not hold true in practice; however, the benefits associated with balance hold approximately even if there are slight imbalances in the number of subjects per experimental condition.) Because they “recycle” subjects while keeping factors mutually orthogonal to each other, balanced factorial designs make very efficient use of experimental subjects. In fact, this means that an increase in the number of factors in a factorial experiment does not necessarily require an increase in the total sample size in order to maintain approximately the same statistical power for testing main effects. This efficiency applies only to main effects, though. For example, given a fixed sample size N , the more experimental conditions there are, the fewer subjects will be in each experimental condition and the less power there will be for, say, pairwise comparisons of particular experimental conditions.

By contrast, the individual experiments approach sometimes requires many more subjects than the complete factorial experiment to obtain a given level of statistical power, because it cannot reuse subjects to test different orthogonal effect estimates simultaneously as balanced factorial experiments can. As Table 4 shows, if a factorial experiment with k factors requires an overall sample size of N to achieve a desired level of statistical power for detecting a main effect of size d at a particular Type I error rate, the comparable individual experiments approach requires kN subjects to detect a simple effect of the same size at the same Type I error rate. This is because the first experiment requires N subjects, the second experiment requires another N subjects, and so on, for a total of kN . In other words, in the individual experiments approach subjects are used in a single experiment to estimate a single effect, and then discarded. The extra subjects provide neither increased Type I error protection nor appreciably increased power, relative to the test of a simple effect in the single factor approach or the test of a main effect in the factorial approach. Unless there is a special need to obtain results from one experiment before beginning another, the extra subjects are largely wasted resources.

As Table 4 shows, if a factorial experiment with k factors requires an overall sample size of N to achieve a desired level of statistical power for detect a main effect of size d at a particular Type I error rate, the comparable single factor approach requires a sample size of ( k + 1)( N /2) to detect a simple effect of the same size at the same Type I error rate. This is because in the single factor approach, to maintain power each mean comparison must be based on two experimental conditions including a total of N subjects. Thus N /2 subjects per experimental condition would be required. However, this single factor experiment would be adequately powered for k simple effects, whereas the comparable factorial experiment with N subjects, although adequately powered for k main effects, would be underpowered for k simple effects. This is because estimating a simple effect in a factorial experiment essentially requires selecting a subset of experimental conditions and discarding the remaining conditions along with the subjects that have been assigned to them. This would bring the sample size considerably below N for each simple effect.

Subject, condition, and overall costs

In order to compare the resource requirements of the four design alternatives it is helpful to draw a distinction between per-subject costs and per-condition overhead costs. Examples of subject costs are recruitment and compensation of human subjects, and housing, feeding and care of laboratory animals. Condition overhead costs refer to costs required to plan, implement, and manage each experimental condition in a design, beyond the cost of the subjects assigned to that condition. Examples of condition overhead costs are training and salaries of personnel to run an experiment, preparation of differing versions of materials needed for different experimental conditions, and cost of setting up and taking down laboratory equipment. Thus, the overhead cost associated with an experimental condition may be either more or less than the cost of a subject. Because the absolute and relative costs in these two domains vary considerably according to the situation, the absolute and relative costs associated with the four designs considered here can vary considerably as well.

One possible scenario is one in which both per-condition overhead costs and per-subject costs are low. For example, consider a social psychology experiment in which experimental conditions consist of different written materials, the experimenters are graduate students on stipends, and a large departmental subject pool is at their disposal. This represents the happy circumstance in which a design can be chosen on purely scientific grounds with little regard to financial costs. Another possible scenario is one in which per-condition overhead costs are low but per-subject costs are high, as might occur if an experiment is to be conducted via the Internet. In this study perhaps adding an experimental condition is a fairly straightforward computer programming task, but substantial cash incentives are required to ensure subject participation. Another example might be an experiment in which individual experimental conditions are not difficult to set up, but the subjects are laboratory animals whose purchase, feeding and care is very costly. Per-condition costs might roughly equal per-subject costs in a similar scenario in which each experimental condition involves time-intensive and complicated reconfiguring of laboratory equipment by a highly-paid technician. Per-condition overhead costs might greatly exceed per-subject costs when subjects are drawn from a subject pool and are not monetarily compensated, but each new experimental condition requires additional training of personnel, preparation of elaborate new materials, or difficult reconfiguration of laboratory equipment.

Comparing relative estimated overall costs across designs

In this section we demonstrate a comparison of relative financial costs across the four design alternatives, based on the expressions in Table 4 . In the demonstration we consider four different situations: effect sizes of d = .2 or d = .5 (corresponding to Cohen's (1988) benchmark values for small and medium, respectively), and k = 6 or k = 10 two-level independent variables. The starting point for the cost comparison is the number of experimental conditions required by each design, and the sample sizes required to achieve statistical power of at least .8 for testing the effect of each factor in the way that seemed appropriate for the design. Specifically, for the full and fractional factorial designs, we calculated the total sample size N needed to have a power of .80 for each main effect. For the individual experiments and single factor designs, we calculated the N needed for a power of .80 for each simple effect of interest. These are shown in Table 5 . As the table indicates, the fractional factorial designs used for k = 6 and k = 10 are both Resolution IV.

Table 5. Number of Experimental Conditions and Sample Size Used to Maintain Per-Factor Power ≥ .8 for Designs in Figures 1 and 2 .

In order to achieve integer n per experimental condition, N is larger than the minimum needed to achieve sufficient power

A practical issue arose that influenced the selection of the overall sample sizes N that are listed in Table 5 . Let N min designate the minimum overall N required to achieve a desired level of statistical power. In the cases marked with an asterisk the overall N that was actually used exceeds N min , because experimental conditions cannot have fractional numbers of subjects. Let n designate the number of subjects in each experimental condition, assuming equal n 's are to be assigned to each experimental condition. In theory the minimum n per experimental condition for a particular design would be N min divided by the number of experimental conditions. However, in some of the cases in Table 5 this would have resulted in a non-integer n . In these cases the per-condition n was rounded up to the nearest integer. For example, consider the complete factorial design with k =10 factors and d = .2. In theory a per-factor power of ≥ .8 would be maintained with N min = 788. However, the complete factorial design required 1024 experimental conditions, so the minimum N that could be used was 1024. All cost comparisons reported here are based on the overall N listed in Table 5 .

For purposes of illustration, per-subject cost will be defined here as the average incremental cost of adding a single research subject to a design without increasing the number of experimental conditions, and condition overhead cost will be defined as the average incremental cost of adding a single experimental condition without increasing the number of subjects. (For simplicity we assume per subject costs do not differ dramatically across conditions.) Then a rough estimate of total costs can be computed as follows, providing a basis for comparing the four design alternatives:

Figure 1 illustrates total costs for experiments corresponding to the situations and designs in Table 5 , for experiments in which per-subject costs equal or exceed per-condition overhead costs. In order to compute total costs on the y -axis, per-condition costs were arbitrarily fixed at $1. Thus the x -axis can be interpreted as the ratio of per-subject costs to per-condition costs; for example, the “4” on the x -axis means that per-subject costs are four times per-condition costs.

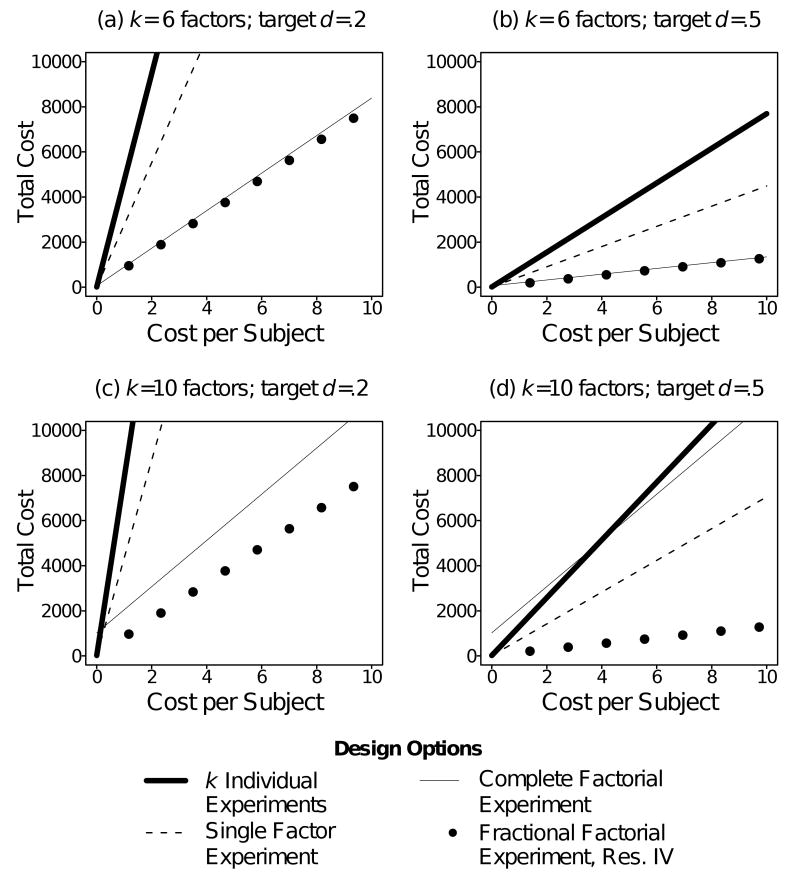
Costs of different experimental design options when per-subject costs exceed per-condition overhead costs. Total costs are computed with per-condition costs fixed at $1.

In the situations considered in Figure 1 , fractional factorial designs were always either least expensive or tied with complete factorial designs for least expensive. As the ratio of per-subject costs to per-condition costs increased, the economy of complete and fractional factorial designs became increasingly evident. Figure 1 shows that when per-subject costs outweighed per-condition costs, the single factor approach and, in particular, the individual experiments approach were often much more expensive than even complete factorial designs, and fractional factorials were often the least expensive.

Figure 2 examines the same situations as in Figure 1 , but now total costs are shown on the y -axis for experiments in which per-condition overhead costs equal or exceed per-subject costs. In order to compute total costs, per-subject costs were arbitrarily fixed at $1. Thus the x -axis represents the ratio of per-condition costs to per-subject costs; in this figure the “40” on the x -axis means that per-condition costs are forty times per-subject costs.

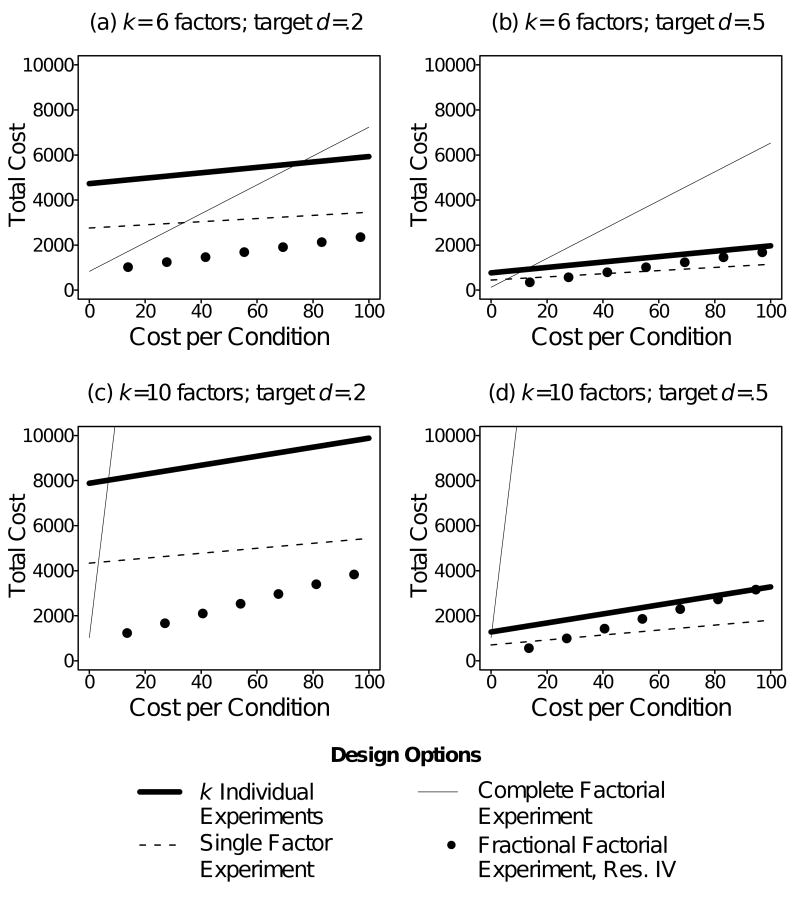
Costs of different experimental design options when per-condition overhead costs exceed per-subject costs. Total costs are computed with per-subject costs fixed at $1.

The picture here is more complex than that in Figure 1 . For the most part, in the four situations considered here the complete factorial was the most expensive design, frequently by a wide margin. The complete factorial requires many more experimental conditions than any of the other design alternatives, so it is not surprising that it was expensive when condition costs were relatively high. It is perhaps more surprising that the individual experiments approach, although it requires many fewer experimental conditions than the complete factorial, was usually the next most expensive. The individual experiments approach even exceeded the cost of the complete factorial under some circumstances when the effect sizes were small. This is because the reduction in experimental conditions afforded by the individual experiments approach was outweighed by much greater subject requirements (see Table 4 ). Figure 2 shows that the least expensive approaches were usually the single factor and fractional factorial designs. Which of these two was less expensive depended on effect size and the ratio of per-condition costs to per-subject costs. When the effect sizes were large and the ratio of per-condition costs to per-subject costs was less than about 20, fractional factorial designs tended to be more economical; the single factor approach was most economical once per-condition costs exceeded about 20 times per-subject costs. However, when effect sizes were small, fractional factorial designs were cheaper until the ratio of per-condition costs to per-subject costs substantially exceeded 100.

A brief tutorial on selecting a fractional factorial design

In this section we provide a brief tutorial intended to familiarize investigators with the basics of choosing a fractional factorial design. The more advanced introduction to fractional factorial designs provided by Kirk (1995) and Kuehl (1999) and the detailed treatment in Wu and Hamada (2000) are excellent resources for further reading.

When the individual experiments and single factor approaches are used, typically the choice of experimental conditions is made on intuitive grounds, with aliasing per se seldom an explicit basis for choosing a design. By contrast, when fractional factorial designs are used aliasing is given primary consideration. Usually a design is selected to achieve a particular aliasing structure while considering cost. Although the choice of experimental conditions for fractional factorials may be less intuitively obvious, this should not be interpreted as meaning that the selection of a fractional factorial design has no conceptual basis. On the contrary, fractional factorial designs are carefully chosen with key research questions in mind.

There are many possible fractional factorial designs for any set of k factors. The designs vary in how many experimental conditions they require and the nature of the aliasing. Fortunately, the hard work of determining the number of experimental conditions and aliasing structure of fractional factorial designs has largely been done. The designs can be found in books (e.g. Box et al., 1978 ; Wu & Hamada, 2000 ) and on the Internet (e.g. National Institute of Standards and Technology/SEMATECH, 2006 ), but the easiest way to choose a fractional factorial design is by using computer software. Here we demonstrate the use of PROC FACTEX ( SAS Institute, Inc., 2004 ). Using this approach the investigator specifies the factors in the experiment, and may specify which effects are in the Estimate, Negligible and Non-negligible categories, the desired design resolution, maximum number of experimental conditions (sometimes called “runs”), and other aspects relevant to choice of a design. The software returns a design that meets the specified criteria, or indicates that such a design does not exist. Minitab (see Ryan, Joiner, & Cryer, 2004 ; Mathews, 2005 ) and S-PLUS ( Insightful Corp., 2007 ) also provide software for designing fractional factorial experiments.

To facilitate the presentation, let us increase the size of the hypothetical example. In addition to the factors (1) choose , (2) breath , and (3) prep , the new six-factor example will also include factors corresponding to whether or not (4) an audience is present besides just the investigator ( audience ); (5) the subject is promised a monetary reward if the speech is judged good enough ( stakes ); and (6) the subject is allowed to speak from notes ( notes ). A complete factorial experiment would require 2 6 = 64 experimental conditions. Three different ways of choosing a fractional factorial design using SAS PROC FACTEX are illustrated below.

Specifying a desired resolution

One way to use software to choose a fractional factorial design is to specify a desired resolution and instruct the software to find the smallest number of experimental conditions needed to achieve it. For example, suppose the investigator in the hypothetical example finds it acceptable to alias main effects with interactions as low as three-way, and to alias two-way interactions with other two-way interactions and higher-order interactions. A design of Resolution IV will meet these criteria and may be requested as follows:

SAS will find a design with these characteristics if it can, print information on the aliasing and design matrix, and save the design matrix in the dataset dataset1. The ALIASING(6) command requests a list of all aliasing up to six-way interactions, and DESIGN asks for the effect codes for each experimental condition in the design to be printed.

Table 6 shows the effect codes from the SAS output for this design. The design found by SAS requires only 16 experimental conditions; that is, the design is a 2 6−2 , or a one-quarter fractional factorial because it requires only 2 −2 = 1/4 = 16/64 of the experimental conditions in the full experiment. In a one-quarter fraction each source of variance has four aliases. This means that each main effect is aliased with three other effects. Because this is a Resolution IV design, all of these other effects are three-way interactions or any higher-order interactions; they will not be main effects or two-way interactions. Similarly, each two-way interaction is aliased with three other effects. Because this is a Resolution IV design, these other effects may be any interactions.

Table 6. An Effect-Coded Design Matrix for a 2 6−2 Fractional Factorial Experiment.

Different fractional factorial designs, even those with the same resolution, have different aliasing structures, some of which may appeal more to an investigator than others. SAS simply returns the first one it can find that fits the desired specifications. There is no feature in SAS, to the best of our knowledge, that automatically returns multiple possible designs with the same resolution, but it is possible to see different designs by arbitrarily changing the order in which the factors are listed in the FACTORS statement. Another possibility is to use the MINABS option to request a design that meets the “minimum aberration” criterion, which is a mathematical definition of least-aliased (see Wu & Hamada, 2000 ).

Specifying which effects are in which categories

The above methods of identifying a suitable fractional factorial design did not require specification of which effects are of primary scientific interest, which are negligible, and which are non-negligible, although the investigator would have to have determined this in order to decide that a Resolution IV design was desired. Another way to identify a fractional factorial design is to specify directly which effects fall in each of these categories, and instruct the software to find the smallest design that does not alias effects of primary interest either with each other or with effects in the non-negligible category. This method enables a little more fine-tuning.

Suppose in addition to the main effects, the investigator wants to be able to estimate all two-way interactions involving breath . The remaining two-way interactions and all three-way interactions are not of scientific interest but may be sizeable, so they are designated non-negligible. In addition, one four-way interaction, breath × prep × notes × stakes might be sizeable, because those factors are suspected in advance to be the most powerful factors, and so their combination might lead to a floor or ceiling effect, which could act as an interaction. This four-way interaction is placed in the non-negligible category. All remaining effects are designated negligible. Given these specifications, a design with the smallest possible number of experimental conditions is desired. The following code will produce such a design:

The ESTIMATE statement designates the effects that are of primary scientific interest and must be aliased only with effects expected to be negligible. The NONNEGLIGIBLE statement designates effects that are not of scientific interest but may be sizeable; these effects must not be aliased with effects mentioned in the ESTIMATE statement. It is necessary to specify only effects to be estimated and those designated non-negligible; any remaining effects are assumed negligible.

The SAS output (not shown) indicates that the result is a 2 6−1 design, which has 32 experimental conditions, and that this design is Resolution VI. Because this design is a one-half fraction of the complete factorial, each source of variation has two aliases, or, in other words, each main effect and interaction is aliased with one other effect. The output provides a complete account of the aliasing, indicating that each main effect is aliased with a five-way interaction, and each two-way interaction is aliased with a four-way interaction. This aliasing is characteristic of Resolution VI designs, as was shown in Table 3 . Because the four-way interaction breath × prep × notes × stakes has been placed in the non-negligible category, the design aliases it with another interaction in this category, audience × choose , rather than with one of the two-way interactions in the Estimate category.

Specifying the maximum number of experimental conditions

Another way to use software to choose a design is to specify the number of experimental conditions in the design, and let the software return the aliasing structure. This approach may make sense when resource constraints impose a strict upper limit on the number of experimental conditions that can be implemented, and the investigator wishes to decide whether key research questions can be addressed within this limit. Suppose in our hypothetical example the investigator can implement no more than eight experimental conditions; in other words, we need a 2 6−3 design. The investigator can use the following code:

In this case, the SAS output suggests a design with Resolution III. Because this Resolution III design is a one-eighth fraction, each source of variance has eight aliases. Each main effect is aliased with seven other effects. These effects may be any interaction; they will not be main effects.

A comparison of results for several different experiments

This section contains direct comparisons among the various experimental designs discussed in this article, based on artificial data generated using the same model for all the designs. This can be imagined as a situation in which after each experiment, time is turned back and the same factors are again investigated with the same experimental subjects, but using a different experimental design.

Let us return to the hypothetical example with six factors (breath , audience , choose , prep , notes , stakes ), each with two levels per factor, coded -1 for Off and +1 for On. Suppose there are a total of 320 subjects, with five subjects randomly assigned to each of the 64 experimental conditions of a 2 6 full factorial design, and the outcome variable is a reverse-scaled questionnaire about public speaking anxiety, that is, a higher score indicates less anxiety. Data were generated so that the score of participant j in the i th experimental condition was modeled as μ i + ε ij where the μ i are given by

and the errors are N (0, 2 2 ). Because the outcome variable in ( 1 ) is reverse-scored, helpful (anxiety-reducing) main effects can be called “positive” and harmful ones can be called “negative.” The standard deviation of 2 was used so that the regression coefficients above can also be interpreted as Cohen's d 's despite the -1/+1 metric for effect coding. Thus, the main effects coefficients in ( 1 ) represent half the long-run average raw difference between participants receiving the Off and On levels of the factor, and also represent the normalized difference between the -1 and +1 groups.

The example was deliberately set up so as not to be completely consistent with the investigator's ideas as expressed in the previous section. In the model above, anxiety is reduced on average by doing the breathing relaxation exercise, by being able to choose one's own topic, by having extra preparation time, and by having notes available. There is a small anxiety-increasing effect of higher stakes. The audience factor had zero main effect on anxiety. The first two positive two-way interactions indicate that longer preparation time intensified the effects of the breathing exercise or notes, or equivalently, that shorter preparation time largely neutralized their effects (as the subjects had little time to put them into practice). The third interaction indicates that higher stakes were energizing for those who were prepared, but anxiety-provoking for the less prepared. The first pair of negative two-way interactions indicate that the breath intervention was somewhat redundant with the more conventional aids of having notes and having one's choice of topic, or equivalently that breathing relaxation was more important when those aids were not available. There follow several other small higher-order nuisance interactions with no clear interpretability, as might occur in practice.

Data were generated using the above model for the following seven experimental designs: Complete factorial; individual experiments; two single factor designs (comparative treatment and constructive treatment); and the Resolution III, IV, and VI designs arrived at in the previous section. The total number of subjects used was held constant at 320 for all of the designs. For the individual experiments approach, six experiments, each with either 53 or 54 subjects, were simulated. For the single factor designs, experiments were simulated assigning either 45 or 46 subjects to each of seven experimental conditions. The comparative treatment design included a no-treatment control (i.e. all factors set to Off) and six experimental conditions, each with one factor set to On and the others set to Off. The constructive treatment design included a no-treatment control and six experimental conditions, each of which added a factor set to On in order from left to right, e.g. in the first treatment condition only breath was set to On, in the second treatment condition breath and audience were set to On and the remaining factors were set to Off, and so on until in the seventh experimental condition all six factors were set to On. To simulate data for the Resolution III, IV, and VI fractional factorial designs, 40, 20, and 10 subjects, respectively, were assigned to each experimental condition. In simulating data for each of the seven design alternatives, the μ i 's were recalculated accordingly but the vector of ε's was left the same.

ANOVA models were fit to each data set in the usual way using SAS PROC GLM. For example, the code used to fit an ANOVA model to the data set corresponding to the Resolution III fractional factorial design was as follows:

This model contained no interactions because they cannot be estimated in a Resolution III design. An abbreviated version of the SAS output corresponding to this code appears in Figure 3 . In the comparative treatment strategy each of the treatment conditions was compared to the no-treatment control. In the constructive treatment strategy each treatment condition was compared to the condition with one fewer factor set to On; for example, the condition in which breath and audience were set to On was compared to the condition in which only breath was set to On.

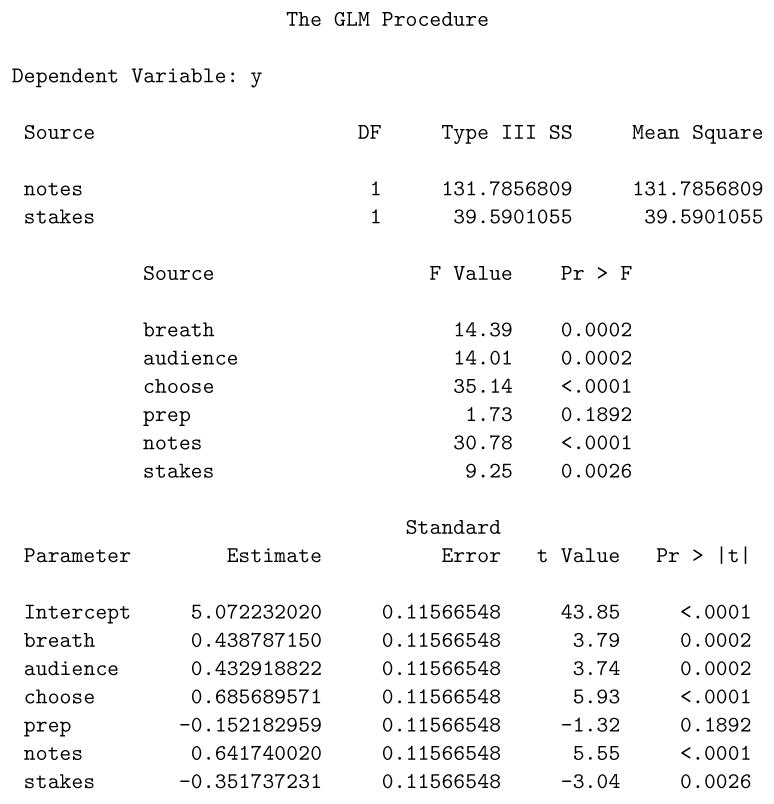
Partial output from SAS PROC GLM for simulated Resolution III data set.

Table 7 contains the regression coefficients corresponding to the effects of each factor for each of the seven designs. For reference, the true values of the regression coefficients used in data generation are shown at the top of the table.

Table 7. Coefficient Estimates for Main Effects under Different Designs in the Simulated Example, with Total Sample Size N = 320.

Coefficient significant at α = .15

Coefficient significant at α = .10

Coefficient significant at α = .05

Coefficient significant at α = .01

Coefficient significant at α = .001

In the complete factorial experiment, breath , choose , prep , and notes were significant. The true main effect of stakes was small; with N = 320 this design had little power to detect it. Audience was marginally significant at α = .15, although the data were generated with this effect set at exactly zero. In the individual experiments approach, only choose was significant, and breath was marginally significant. The results for the comparative treatment experiment were similar to those of the individual experiments approach, as would be expected given that the two have identical aliasing. An additional effect was marginally significant in the comparative treatment approach, reflecting the additional statistical power associated with this design as compared to the individual experiments approach. In the constructive treatment experiment none of the factors were significant at α = .05. There were two marginally significant effects, breath and notes .

In the Resolution III design every effect except prep was significant. One of these, the significant effect of audience , was a spurious result (probably caused by aliasing with the prepare × stakes interaction). By contrast, results of the Resolution IV and VI designs were very similar to those of the complete factorial, except that in the Resolution VI design stakes was significant. In the individual experiments and single factor approaches, the estimates of the coefficients varied considerably from the true values. In the fractional factorial designs the estimates of the coefficients tended to be closer to the true values, particularly in the Resolution IV and Resolution VI designs.

Table 8 shows estimates of interactions from the designs that enable such estimates, namely the complete factorial design and the Resolution IV and Resolution VI factorial designs. The breath × prep interaction was significant in all three designs. The breath × choose interaction was significant in the complete factorial and the Resolution VI fractional factorial but was estimated as zero in the Resolution IV design. In general the coefficients for these interactions were very similar across the three designs. An exception was the coefficient for the breath × choose interaction, and, to a lesser degree, the coefficient for the breath × notes interaction.

Table 8. Coefficient Estimates for Selected Interactions under Different Designs in the Simulated Example, with Total Sample Size N = 320.

Differences observed among the designs in estimates of coefficients are due to differences in aliasing plus a minor random disturbance due to reallocating the error terms when each new experiment was simulated, as described above. In general, more aliasing was associated with greater deviations from the true coefficient values. No effects were aliased in the complete factorial design, which had coefficient estimates closest to the true values. In the Resolution IV design each effect was aliased with three other effects, all of them interactions of three or more factors, and in the Resolution VI design each effect was aliased with one other effect, an interaction of four or more factors. These designs had coefficient estimates that were also very close to the true values. The Resolution III fractional factorial design, which aliased each effect with seven other effects, had coefficient estimates somewhat farther from the true values. The coefficient estimates associated with the individual and single factor approaches were farthest from the true values of the main effect coefficients. In the individual experiments and single factor approaches each effect was aliased with 15 other effects (the main effect of a factor was aliased with all the interactions involving that factor, from the two-way up to the six-way). The comparative treatment and constructive treatment approach aliased the same number of effects but differed in the coding of the aliased effects (as can be seen in Table 2 ), which is why their coefficient estimates differed.

Although the seven experiments had the same overall sample size N , they differed in statistical power. The complete and fractional factorial experiments, which had identical statistical power, were the most powerful. Next most powerful were the comparative treatment and constructive treatment designs. The individual experiments approach was the least powerful. These differences in statistical power, along with the differences in coefficient estimates, were reflected in the effects found significant at various levels of α across the designs. Among the designs examined here, the individual experiments approach and the two single factor designs showed the greatest disparities with the complete factorial.

Given the differences among them in aliasing, it is perhaps no surprise that these designs yielded different effect estimates and hypothesis tests. The research questions that motivate individual experiments and single factor designs, which often involve pairwise contrasts between individual experimental conditions, may not require estimation of main effects per se , so the relatively large differences between the coefficient estimates obtained using these designs and the true main effect coefficients may not be important. Instead, what may be more noteworthy is how few effects these designs detected as significant as compared to the factorial experiments.

General discussion

Some overall recommendations.

Despite the situation-specific nature of most design decisions, it is possible to offer some general recommendations. When per-subject costs are high in relation to per-condition overhead costs, complete and fractional factorials are usually the most economical designs. When per-condition costs are high in relation to per-subject costs, usually either a fractional factorial or single factor design will be most economical. Which is most economical will depend on considerations such as the number of factors, the sample size required to achieve the desired statistical power, and the particular fractional factorial design being considered.

In the limited set of situations examined in this article, the individual experiments approach emerged as the least economical. Although the individual experiments approach requires many fewer experimental conditions than a complete factorial and usually requires fewer than a fractional factorial, it requires more experimental conditions than a single factor experiment. In addition, it makes the least efficient use of subjects of any of the designs considered in this article. Of course, an individual experiments approach is necessary whenever the results of one experiment must be obtained first in order to inform the design of a subsequent experiment. Except for this application, in general the individual experiments approach is likely to be the least appealing of the designs considered here. Investigators who are planning a series of individual experiments may wish to consider whether any of them can be combined to form a complete or fractional factorial experiment, or whether a single factor design can be used.

Although factorial experiments with more than two or three factors are currently relatively rare in psychology, we recommend that investigators give such designs serious consideration. All else being equal, the statistical power of a balanced factorial experiment to detect a main effect of a given size is not reduced by the presence of other factors, except to a small degree caused by the reduction of error degrees of freedom in the model. In other words, if main effects are of primary scientific interest and interactions are not of great concern, then factors can be added without needing to increase N appreciably.

An interest in interactions is not the only reason to consider using factorial designs; investigators may simply wish to take advantage of the economy these designs afford, even when interactions are expected to be negligible or are not of scientific interest. In particular, investigators who undergo high subject costs but relatively modest condition costs may find that a factorial experiment will be much more economical than other design alternatives. Investigators faced with an upper limit on the availability of subjects may even find that a factorial experiment enables them to investigate research questions that would otherwise have to be set aside for some time. As Oehlert (2000 , p. 171) explained, “[t]here are thus two times when you should use factorial treatment structure—when your factors interact, and when your factors do not interact.”

One of the objectives of this article has been to demonstrate that fractional factorial designs merit consideration for use in psychological research alongside other reduced designs and complete factorial designs. Previous authors have noted that fractional factorial designs may be useful in a variety of areas within the social and behavioral sciences ( Landsheer & van den Wittenboer, 2000 ) such as behavioral medicine (e.g. Allore, Peduzzi, Han, & Tinetti, 2006 ; Allore, Tinettia, Gill, & Peduzzi, 2005 ), marketing research (e.g. Holland & Cravens, 1973 ), epidemiology ( Taylor et al., 1994 ), education ( McLean, 1966 ), human factors ( Simon & Roscoe, 1984 ), and legal psychology ( Stolle, Robbennolt, Patry, & Penrod, 2002 ). Shaw (2004) and Shaw, Festing, Peers, & Furlong (2002) noted that factorial and fractional factorial designs can help to reduce the number of animals that must be used in laboratory research. Cutler, Penrod, and Martens (1987) used a large fractional factorial design to conduct an experiment studying the effect of context variables on the ability of participants to identify the perpetrator correctly in a video of a simulated robbery. Their experiment included 10 factors, with 128 experimental conditions, but only 290 subjects.

An important special case: Development and evaluation of behavioral interventions

As discussed by Allore et al. (2006) , Collins, Murphy, Nair, and Strecher (2005) , Collins, Murphy, and Strecher (2007) , and West et al. (1993) , behavioral intervention scientists could build more potent interventions if there was more empirical evidence about which intervention components are contributing to program efficacy, which are not contributing, and which may be detracting from overall efficacy. However, as these authors note, generally behavioral interventions are designed a priori and then evaluated by means of the typical randomized controlled trial (RCT) consisting of a treatment group and a control group (e.g. experimental conditions 8 and 1, respectively, in Table 2 ). This all-or-nothing approach, also called the treatment package strategy ( West et al., 1993 ), involves the fewest possible experimental conditions, so in one sense it is a very economical design. The trade-off is that all main effects and interactions are aliased with all others. Thus although the treatment package strategy can be used to evaluate whether an intervention is efficacious as a whole, it does not provide direct evidence about any individual intervention component. A factorial design with as many factors as there are distinct intervention components of interest would provide estimates of individual component effects and interactions between and among components.

Individual intervention components are likely to have smaller effect sizes than the intervention as a whole ( West & Aiken, 1997 ), in which case sample size requirements will be increased as compared to a two-experimental-condition RCT. One possibility is to increase power by using a Type I error rate larger than the traditional α = .05, in other words, to tolerate a somewhat larger probability of mistakenly choosing an inactive component for inclusion in the intervention in order to reduce the probability of mistakenly rejecting an active intervention component. Collins et al. (2005 , 2007) recommended this and similar tactics as part of a phased experimental strategy aimed at selecting components and levels to comprise an intervention. In this phased experimental strategy, after the new intervention is formed its efficacy is confirmed in a RCT at the conventional α = .05. As Hays (1994 , p. 284) has suggested, “In some situations, perhaps, we should be far more attentive to Type II errors and less attentive to setting α at one of the conventional levels.”

One reason for eschewing a factorial design in favor of the standard two-experimental-condition RCT may be a shortage of resources needed to implement all the experimental conditions in a complete factorial design. If this is the primary obstacle, it is possible that it can be overcome by identifying a fractional factorial design requiring a manageable number of experimental conditions. Fractional factorial designs are particularly apropos for experiments in which the primary objective is to determine which factors out of an array of factors have important effects (where “important” can be defined as “statistically significant,” “effect size greater than d ,” or any other reasonable empirical criterion). In engineering these are called screening experiments. For example, suppose an investigator is developing an intervention and wishes to conduct an experiment to ascertain which of a set of possible intervention features are likely to contribute to an overall intervention effect. In most cases an approximate estimate of the effect of an individual factor is sufficient for a screening experiment, as long as the estimate is not so far off as to lead to incorrect inclusion of an intervention feature that has no effect (or, worse, has a negative effect) or incorrect exclusion of a feature that makes a positive contribution. Thus in this context the increased scientific information that can be gained using a fractional factorial design may be an acceptable tradeoff against the somewhat reduced estimation precision that can accompany aliasing. (For a Monte Carlo simulation examining the use of a fractional factorial screening experiment in intervention science, see Collins, Chakroborty, Murphy, & Strecher, in press .)

It must be acknowledged that even very economical fractional factorial designs typically require more experimental conditions than intervention scientists routinely consider implementing. In some areas in intervention science, there may be severe restrictions on the number of experimental conditions that can be realistically handled in any one experiment. For example, it may not be reasonable to demand of intervention personnel that they deliver different versions of the intervention to different subsets of participants, as would be required in any experiment other than the treatment package RCT. Or, the intervention may be so complex and demanding, and the context in which it must be delivered so chaotic, that implementing even two experimental conditions well is a remarkable achievement, and trying to implement more would surely result in sharply diminished implementation fidelity ( West & Aiken, 1997 ). Despite the undeniable reality of such difficulties, we wish to suggest that they do not necessarily rule out the use of complete and, in particular, fractional factorial designs across the board in all areas of intervention science. There may be some areas in which a careful analysis of available resources and logistical strategies will suggest that a factorial approach is feasible. One example is Strecher et al. (2008) , who described a 16-experimental-condition fractional factorial experiment to investigate five intervention components in a smoking cessation intervention. Another example can be found in Nair et al. (2008) , who described a 16-experimental-condition fractional factorial experiment to investigate five features of decision aids for women choosing among breast cancer treatments. Commenting on the Strecher et al. article, Norman (2008) wrote, “The fractional factorial design can provide considerable cost savings for more rapid prototype testing of intervention components and will likely be used more in future health behavior change research” (p. 450). Collins et al. (2005) and Nair et al. (2008) have provided some introductory information on the use of fractional factorial designs in intervention research. Collins et al. (2005 , 2007) discussed the use of fractional factorial designs in the context of a phased experimental strategy for building more efficacious behavioral interventions.

One interesting difference between the RCT on the one hand and factorial and fractional factorial designs on the other is that as compared to the standard RCT, a factorial design assigns a much smaller proportion of subjects to an experimental condition that receives no treatment. In a standard two-arm RCT about half of the experimental subjects will be assigned to some kind of control condition, for example a wait list or the current standard of care. By contrast, in a factorial experiment there is typically only one experimental condition in which all of the factors are set to Off. Thus if the design is a 2 3 factorial, say, seventh-eighths of the subjects will be assigned to a condition in which at least one of the factors is set to On. If the intervention is sought-after and assignment to a control condition is perceived as less desirable than assignment to a treatment condition, there may be better compliance because most subjects will receive some version of an intervention. In fact, it often may be possible to select a fractional factorial design in which there is no experimental condition in which all factors are set to Off.

Investigating interactions between individual characteristics and experimental factors in factorial experiments

Investigators are often interested in determining whether there are interactions between individual subject characteristics and any of the factors in a factorial or fractional factorial experiment. As an example, suppose an investigator is interested in determining whether gender interacts with the six independent variables in the hypothetical example used in this article. There are two ways this can be accomplished; one is exploratory, and the other is a priori (e.g. Murray, 1998 ).

In the exploratory approach, after the experiment has been conducted gender is coded and added to the analysis of variance as if it were another factor. Even if the design was originally perfectly balanced, such an addition nearly always results in a substantial disruption of balance. Thus the effect estimates are unlikely to be orthogonal, and so care must be taken in estimating the sums of squares. If a reduced design was used, it is important to be aware of what effects, if any, are aliased with the interactions being examined. In most fractional factorial experiments the two-way interactions between gender and any of the independent variables are unlikely to be aliased with other effects, but three-way and higher-order interactions involving gender are likely to be aliased with other effects.

In the a priori approach, gender is built into the design as an additional factor before the experiment is conducted, by ensuring that it is crossed with every other factor. Orthogonality will be maintained and power for detecting gender effects will be optimized if half of the subjects are male and half are female, with randomization done separately within each gender, as if gender were a blocking variable. However, in blocking it is assumed that there are no interactions between the blocking variable and the independent variables; the purpose of blocking is to control error. By contrast, in the a priori approach the interactions between gender and the manipulated independent variables are of particular interest, and the experiment should be powered accordingly to detect these interactions. As compared to the exploratory approach, with the a priori approach it is much more likely that balance can be maintained or nearly maintained. Variables such as gender can easily be incorporated into fractional factorial designs using the a priori approach. These variables can simply be listed with the other independent variables when using software such as PROC FACTEX to identify a suitable fractional factorial design. A fractional factorial design can be chosen so that important two-way and even three-way interactions between, for example, gender and other independent variables are aliased only with higher-order interactions.

How negligible is negligible?

To the extent that an effect placed in the negligible category is nonzero, the estimate of any effect of primary scientific interest that is aliased with it will be different from an estimate based on a complete factorial experiment. Thus a natural question is, “How small should the expected size of an interaction be for the interaction to be placed appropriately in the negligible category?”

The answer depends on the field of scientific endeavor, the value of the scientific information that can be gained using a reduced design, and the kind of decisions that are to be made based on the results of the experiment. There are risks associated with assuming an effect is negligible. If the effect is in reality non-negligible and positive, it can make a positive effect aliased with it look spuriously large, or make a negative effect aliased with it look spuriously zero or even positive. If an effect placed in the negligible category is non-negligible and negative, it can make a positive effect aliased with it look spuriously zero or even negative, or make a negative effect aliased with it look spuriously large.

Placing an effect in the negligible category is not the same as assuming it is exactly zero. Rather, the assumption is that the effect is small enough not to be very likely to lead to incorrect decisions. If highly precise estimates of effects are required, it may be that few or no effects are deemed small enough to be eligible for placement in the negligible category. If the potential gain of additional scientific information obtained at a cost of fewer resources offsets the risk associated with reduced estimation precision and the possibility of some spurious effects, then effects expected to be nonzero, but small, may more readily be designated negligible.

Some limitations of this article

The discussion of reduced designs in this article is limited in a number of ways. One limitation of the discussion is that it has focused on between-subjects designs. It is straightforward to extend every design here to incorporate repeated measures, which will improve statistical power. However, all else being equal, the factorial designs will still have more power than the individual experiments and single factor approaches. There have been a few examples of the application of within-subjects fractional designs in legal psychology ( Cutler, Penrod, & Dexter, 1990 ; Cutler, Penrod, & Martens, 1987 ; Cutler, Penrod, & Stuve, 1988 ; O'Rourke, Penrod, Cutler, & Stuve, 1989 ; Smith, Penrod, Otto, & Park, 1996 ) and in other research on attitudes and choices (e.g., van Schaik, Flynn & van Wersch, 2005 ; Sorenson & Taylor, 2005 ; Zimet et al., 2005 ) in which a fractional factorial structure is used to construct the experimental conditions assigned to each subject. In fact, the Latin squares approach for balancing orders of experimental conditions in repeated-measures studies is a form of within-subjects fractional factorial. Within-subjects fractional designs of this kind could be seen as a form of planned missingness design (see Graham, Taylor, Olchowski, & Cumsille, 2006 ).

Another limitation of this article is the focus on factors with only two levels. Designs involving exclusively two-level factors are very common, and factorial designs with two levels per factor tend to be more economical than those involving factors with three or more levels, as well as much more interpretable in practice, due to their simpler interaction structure ( Wu & Hamada, 2000 ). However, any of the designs discussed here can incorporate factors with more than two levels, and different factors may have different numbers of levels. Factors with three or more levels, and in particular an array of factors with mixed numbers of levels, adds complexity to the aliasing in fractional factorial experiments. Although this requires careful attention, it can be handled in a straightforward manner using software like SAS PROC FACTEX.

This article has not discussed what to do when unexpected difficulties arise. One such difficulty is unplanned missing data, for example, an experimental subject failing to provide outcome data. The usual concerns about informative missingness (e.g. dropout rates that are higher in some experimental conditions than in others) apply in complete and reduced factorial experiments just as they do in other research settings. In any complete or reduced design unplanned missingness can be handled in the usual manner, via multiple imputation or maximum likelihood (see e.g. Schafer & Graham, 2002 ). If experimental conditions are assigned unequal numbers of subjects, use of a regression analysis framework can deal with the resulting lack of orthogonality of effects with very little extra effort (e.g. PROC GLM in SAS). Another unexpected difficulty that can arise in reduced designs is evidence that assumptions about negligible interactions are incorrect. If this occurs, one possibility is to implement additional experimental conditions to address targeted questions, in an approach often called sequential experimentation ( Meyer, Steinberg, & Box, 1996 ).

The resource management perspective: Strategic weighing of resource requirements and expected scientific benefit

According to the resource management perspective, the choice of an experimental design requires consideration of both resource requirements and expected scientific benefit; the preferred research design is the one expected to provide the greatest scientific benefit in relation to resources required. Although aliasing may sometimes be raised as an objection to the use of fractional factorial designs, it must be remembered that aliasing in some form is inescapable in any and all reduced designs, including individual experiments and single factor designs. We recommend considering all feasible designs and making a decision taking a resource management perspective that weighs resource demands against scientific costs and benefits.

Paramount among the considerations that drive the choice of an experimental design is addressing the scientific question motivating the research. At the same time, if this scientific question can be addressed only by a very resource-intensive design, but a closely related question can be addressed by a much less resource-intensive design, the investigator may wish to consider reframing the question to conserve resources. For example, when research subjects are expensive or scarce, it may be prudent to consider whether scientific questions can be framed in terms of main effects rather than simple effects so that a factorial or fractional factorial design can be used. Or, when resource limitations preclude implementing more than a very few experimental conditions, it may be prudent to consider framing research questions in terms of simple effects rather than main effects. When a research question is reframed to take advantage of the economy offered by a particular design, it is important that the interpretation of effects be consistent with the reframing, and that this consistency be maintained not only in the original research report but in subsequent citations of the report, as well as integrative reviews or meta-analyses that include the findings.

Resource requirements can often be estimated objectively, as discussed above. Tables like Table 5 may be helpful and can readily be prepared for any N and k . (A SAS macro to perform these computations can be found on the web site http:\\methodology.psu.edu .) In contrast, assessment of expected scientific benefit is much more subjective, because it represents the investigator's judgment of the value of the scientific knowledge proffered by an experimental design in relation to the plausibility of any assumptions that must be made. For this reason, weighing resource requirements against expected scientific benefit can be challenging. Because expected scientific benefit usually cannot be expressed in purely financial terms, or even readily quantified, a simple benefit to cost ratio is unlikely to be helpful in choosing among alternative designs. For many social and behavioral scientists, the decision may be simplified somewhat by the existence of absolute upper limits on the number of subjects that are available, number of experimental conditions that can be handled logistically, availability of qualified personnel to run experimental conditions, number of hours shared equipment can be used, and so on. Designs that would exceed these limitations are immediately ruled out, and the preferred design now becomes the one that is expected to provide the greatest scientific benefit without exceeding available resources. This requires careful planning to ensure that the design of the study clearly addresses the scientific questions of most interest.

For example, suppose an investigator who is interested in six two-level independent variables has the resources to implement an experiment with at most 16 experimental conditions. One possible strategy is a “complete” factorial design involving four factors and holding the remaining two factors constant at specified levels. Given that six factors are of scientific interest, this “complete” factorial design is actually a reduced design. This approach enables estimation of the main effects and all interactions involving the four factors included in the experiment, but these effects will be aliased with interactions involving the two omitted factors. Therefore in order to draw conclusions either these effects must be assumed negligible, or interpretation must be restricted to the levels at which the two omitted factors were set. Another possible strategy is a Resolution IV fractional factorial design including all six factors, which enables investigation of all six main effects and many two-way interactions, but no higher-order interactions. Instead, this design requires assuming that all three-way and higher-order interactions are negligible. Thus, both designs can be implemented within available resources, but they differ in the kind of scientific information they provide and the assumptions they require. Which option is better depends on the value of the information provided by each experiment in relation to the research questions. If the ability to estimate the higher-order interactions afforded by the four-factor factorial design is more valuable than the ability to estimate the six main effects and additional two-way interactions afforded by the fractional factorial design, then the four-factor factorial may have greater expected scientific benefit. On the other hand, if the investigator is interested primarily in main effects of all six factors and selected two-way interactions, the fractional factorial design may provide more valuable information.

Strategic use of reduced designs involves taking calculated risks. To assess the expected scientific benefit of each design, the investigator must also consider the risk associated with any necessary assumptions in relation to the value of the knowledge that can be gained by the design. In the example above, any risk associated with making the assumptions required by the fractional factorial design must be weighted against the value associated with the additional main effect and two-way interaction estimates. If other, less powerful reduced designs are considered, any increased risk of a Type II error must also be considered. If an experiment is an exploratory endeavor intended to determine which factors merit further study in a subsequent experiment, the ability to investigate many factors may be of paramount importance and may outweigh the risks associated with aliasing. A design that requires no or very safe assumptions may not have a greater net scientific benefit than a riskier design if the knowledge it proffers is meager or is not at the top of the scientific agenda motivating the experiment. Put another way, the potential value of the knowledge that can be gained in a design may offset any risk associated with the assumptions it requires.

Acknowledgments

The authors would like to thank Bethany C. Bray, Michael J. Cleveland, Donna L. Coffman, Mark Feinberg, Brian R. Flay, John W. Graham, Susan A. Murphy, Megan E. Patrick, Brittany Rhoades, and David Rindskopf for comments on an earlier draft. This research was supported by NIDA grants P50 DA10075 and K05 DA018206.

Assuming orthogonality is maintained, adding a factor to a factorial experiment does not change estimates of main effects and interactions. However, the addition of a factor does change estimates of error terms, so hypothesis tests can be slightly different.

In the social and behavioral sciences literature the term “fractional factorial” has sometimes been applied to reduced designs that do not maintain the balance property, such as the individual experiments and single factor designs. In this article we maintain the convention established in the statistics literature (e.g. Wu & Hamada, 2000 ) of reserving the term “fractional factorial” for the subset of reduced designs that maintain the balance property.

Contributor Information

Linda M. Collins, The Methodology Center and Department of Human Development and Family Studies, The Pennsylvania State University

John J. Dziak, The Methodology Center, The Pennsylvania State University

Runze Li, Department of Statistics and The Methodology Center, The Pennsylvania State University.

• Allore H, Peduzzi P, Han L, Tinetti M. Using the SAS system for experimental designs for multicomponent interventionsin medicine (No. 127-31) SAS white paper. 2006 see www2.sas.com/proceedings/sugi31/127-31.pdf .
• Allore HG, Tinettia ME, Gill TM, Peduzzi PN. Experimental designs for multicomponent interventions among persons with multifactorial geriatric syndromes. Clinical Trials. 2005;2:13–21. doi: 10.1191/1740774505cn067oa. [ DOI ] [ PubMed ] [ Google Scholar ]
• Bolger N, Amarel D. Effects of social support visibility on adjustment to stress: Experimental evidence. Journal of Personality and Social Psychology. 2007;92:458–475. doi: 10.1037/0022-3514.92.3.458. [ DOI ] [ PubMed ] [ Google Scholar ]
• Box G, Hunter JS. The 2k−p fractional factorial designs. Technometrics. 1961;3:311–351. 449–458. [ Google Scholar ]
• Box G, Meyer R. An analysis for unreplicated fractional factorials. Technometrics. 1986;28:11–18. [ Google Scholar ]
• Box GEP, Hunter WG, Hunter JS. Statistics for experimenters: An introduction to design, data analysis, and model building. New York: Wiley; 1978. [ Google Scholar ]
• Cohen J. Statistical power analysis for the behavioral sciences. Mahwah, NJ: Lawrence Erlbaum Associates; 1988. [ Google Scholar ]
• Collins L, Chakroborty B, Murphy S, Strecher V. Comparison of a phased experimental approach and a single randomized clinical trial for developing multicomponent behavioral interventions. Clinical Trials. doi: 10.1177/1740774508100973. in press. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Collins LM, Murphy SA, Nair V, Strecher V. A strategy for optimizing and evaluating behavioral interventions. Annals of Behavioral Medicine. 2005;30:65–73. doi: 10.1207/s15324796abm3001_8. [ DOI ] [ PubMed ] [ Google Scholar ]
• Collins LM, Murphy SA, Strecher V. The Multiphase Optimization Strategy (MOST) and the SequentialMultiple Assignment Randomized Trial (SMART): New methods formore potent e-health interventions. American Journal of Preventive Medicine. 2007;32:S112–S118. doi: 10.1016/j.amepre.2007.01.022. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Cutler BL, Penrod SD, Dexter HR. Juror sensitivity to eyewitness identification evidence. Law and Human Behavior. 1990;14:185–191. [ Google Scholar ]
• Cutler BL, Penrod SD, Martens TK. Improving the reliability of eyewitness identification: Putting context into context. Journal of Applied Psychology. 1987;71:629–637. [ Google Scholar ]
• Cutler BL, Penrod SD, Stuve TE. Juror decision making in eyewitness identification cases. Law and Human Behavior. 1988;12:41–55. [ Google Scholar ]
• Graham JW, Taylor BJ, Olchowski AE, Cumsille PE. Planned missing data designs in psychological research. Psychological Methods. 2006;11:323–343. doi: 10.1037/1082-989X.11.4.323. [ DOI ] [ PubMed ] [ Google Scholar ]
• Green PE, Rao VR. Conjoint measurement for quantifying judgmental data. Journal of Marketing Research. 1971;8:355–363. [ Google Scholar ]
• Hays WL. Statistics. Orlando, Florida: Harcourt Brace & Company; 1994. [ Google Scholar ]
• Holland CW, Cravens DW. Fractional factorial experimental designs in marketing research. Journal of Marketing Research. 1973;10:270–276. [ Google Scholar ]
• Insightful Corporation. S-PLUS® 8 for Windows® user's guide. Seattle, WA: Insightful Corporation; 2007. [ Google Scholar ]
• Kirk R. Experimental design: Procedures for the behavioral sciences. 3rd. Pacific Grove, CA: Brooks/Cole; 1995. [ Google Scholar ]
• Kuehl RO. Design of experiments: Statistical principles of research design and analysis. 2nd. Pacific Grove, CA: Duxbury/Thomson; 1999. [ Google Scholar ]
• Landsheer JA, van den Wittenboer G. Fractional designs: a simulation study of usefulness in the social sciences. Behavior Research Methods. 2000;32:528–36. doi: 10.3758/bf03200825. [ DOI ] [ PubMed ] [ Google Scholar ]
• Mathews PG. Design of experiments with Minitab. Milwaukee, WI: Quality Press; 2005. [ Google Scholar ]
• McLean LD. Phantom classrooms. The School Review. 1966;74:139–149. [ Google Scholar ]
• Meyer RD, Steinberg DM, Box GEP. Follow-up designs to resolve confounding in multifactor experiments. Technometrics. 1996;38:303–313. [ Google Scholar ]
• Murray DM. Design and analysis of group-randomized trials. New York: Oxford University Press; 1998. [ Google Scholar ]
• Nair V, Strecher V, Fagerlin A, Ubel P, Resnicow K, Murphy S, et al. Screening Experiments and the Use of Fractional Factorial Designs in Behavioral Intervention Research. American Journal of Public Health. 2008;98(8):1354. doi: 10.2105/AJPH.2007.127563. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• National Institute of Standards and Technology/SEMATECH. e-Handbook of statistical methods. [July 17, 2007];2006 http://www.itl.nist.gov/div898/handbook/ Available from http://www.itl.nist.gov/div898/handbook/
• Norman GJ. Answering the “What works?” question in health behavior change. American Journal of Preventive Medicine. 2008;34:449–450. doi: 10.1016/j.amepre.2008.02.005. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Oehlert GW. A first course in design and analysis of experiments. New York: W. H. Freeman; 2000. [ Google Scholar ]
• O'Rourke TE, Penrod SD, Cutler BL, Stuve TE. The external validity of eyewitness identification research: Generalizing across subject populations. Law and Human Behavior. 1989;13:385–398. [ Google Scholar ]
• Ryan BF, Joiner BL, Cryer JD. Minitab handbook. 5th. Belmont, CA: Duxbury/Thomson; 2004. [ Google Scholar ]
• SAS Institute Inc. SAS/QC® 9.1 user's guide. Cary, NC: Author; 2004. [ Google Scholar ]
• Schafer JL, Graham JW. Missing data: Our view of the state of the art. Psychological Methods. 2002;7:147–177. [ PubMed ] [ Google Scholar ]
• Shaw R. Reduction in laboratory animal use by factorial design. Alternatives to Laboratory Animals. 2004;32:49–51. doi: 10.1177/026119290403202s10. [ DOI ] [ PubMed ] [ Google Scholar ]
• Shaw R, Festing MFW, Peers I, Furlong L. Use of factorial designs to optimize animal experiments and reduce animal use. Institute for Laboratory Animal Research Journal. 2002;43:223–232. doi: 10.1093/ilar.43.4.223. [ DOI ] [ PubMed ] [ Google Scholar ]
• Simon CW, Roscoe SN. Application of a multifactor approach to transfer of training research. Human Factors. 1984;26:591–612. [ Google Scholar ]
• Smith BC, Penrod SD, Otto AL, Park RC. Jurors' use of probabilistic evidence. Law and Human Behavior. 1996;20:49–82. [ Google Scholar ]
• Sorenson SB, Taylor CA. Female aggression toward male intimate partners: An examination of social norms in a community-based sample. Psychology of Women Quarterly. 2005;29:78–96. [ Google Scholar ]
• Stolle DP, Robbennolt JK, Patry M, Penrod SD. Fractional factorial designs for legal psychology. Behavioral Sciences and the Law. 2002;20:5–17. doi: 10.1002/bsl.475. [ DOI ] [ PubMed ] [ Google Scholar ]
• Strecher VJ, McClure JB, Alexander GL, Chakraborty B, Nair VN, Konkel JM, et al. Web-based smoking-cessation programs: Results of a randomized trial. American Journal of Preventive Medicine. 2008;34:373–381. doi: 10.1016/j.amepre.2007.12.024. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Taylor PR, Li B, Dawsey SM, Li J, Yang CS, Gao W, et al. Prevention of esophageal cancer: The nutrition intervention trials in Linxian, China. Cancer Research. 1994;54:2029s–2031s. [ PubMed ] [ Google Scholar ]
• van Schaik P, Flynn D, van Wersch A. Influence of illness script components and medical practice on medical decision making. Journal of Experimental Psychology: Applied. 2005;11:187–199. doi: 10.1037/1076-898X.11.3.187. [ DOI ] [ PubMed ] [ Google Scholar ]
• West SG, Aiken LS. Toward understanding individual effects in multicomponent prevention programs: Design and analysis strategies. In: Bryant K, Windle M, West S, editors. The science of prevention: Methodological advances from alcohol and substanceabuse research. Washington, D.C.: American Psychological Association; 1997. pp. 167–209. chap 6. [ Google Scholar ]
• West SG, Aiken LS, Todd M. Probing the effects of individual components in multiple component prevention programs. American Journal of Community Psychology. 1993;21:571–605. doi: 10.1007/BF00942173. [ DOI ] [ PubMed ] [ Google Scholar ]
• Wu C, Hamada M. Experiments: Planning, analysis, and parameter design optimization. New York: Wiley; 2000. [ Google Scholar ]
• Zimet GD, Mays RM, Sturm LA, Ravert AA, Perkins SM, Juliar BE. Parental attitudes about sexually transmitted infection vaccination for their adolescent children. Archives of Pediatrics and Adolescent Medicine. 2005;159:132–137. doi: 10.1001/archpedi.159.2.132. [ DOI ] [ PubMed ] [ Google Scholar ]
• View on publisher site
• PDF (1.1 MB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections

Experimental Design: Types, Examples & Methods

Saul McLeod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

Experimental design refers to how participants are allocated to different groups in an experiment. Types of design include repeated measures, independent groups, and matched pairs designs.

Probably the most common way to design an experiment in psychology is to divide the participants into two groups, the experimental group and the control group, and then introduce a change to the experimental group, not the control group.

The researcher must decide how he/she will allocate their sample to the different experimental groups.  For example, if there are 10 participants, will all 10 participants participate in both groups (e.g., repeated measures), or will the participants be split in half and take part in only one group each?

Three types of experimental designs are commonly used:

1. Independent Measures

Independent measures design, also known as between-groups , is an experimental design where different participants are used in each condition of the independent variable.  This means that each condition of the experiment includes a different group of participants.

This should be done by random allocation, ensuring that each participant has an equal chance of being assigned to one group.

Independent measures involve using two separate groups of participants, one in each condition. For example:

• Con : More people are needed than with the repeated measures design (i.e., more time-consuming).
• Pro : Avoids order effects (such as practice or fatigue) as people participate in one condition only.  If a person is involved in several conditions, they may become bored, tired, and fed up by the time they come to the second condition or become wise to the requirements of the experiment!
• Con : Differences between participants in the groups may affect results, for example, variations in age, gender, or social background.  These differences are known as participant variables (i.e., a type of extraneous variable ).
• Control : After the participants have been recruited, they should be randomly assigned to their groups. This should ensure the groups are similar, on average (reducing participant variables).

2. Repeated Measures Design

Repeated Measures design is an experimental design where the same participants participate in each independent variable condition.  This means that each experiment condition includes the same group of participants.

Repeated Measures design is also known as within-groups or within-subjects design .

• Pro : As the same participants are used in each condition, participant variables (i.e., individual differences) are reduced.
• Con : There may be order effects. Order effects refer to the order of the conditions affecting the participants’ behavior.  Performance in the second condition may be better because the participants know what to do (i.e., practice effect).  Or their performance might be worse in the second condition because they are tired (i.e., fatigue effect). This limitation can be controlled using counterbalancing.
• Pro : Fewer people are needed as they participate in all conditions (i.e., saves time).
• Control : To combat order effects, the researcher counter-balances the order of the conditions for the participants.  Alternating the order in which participants perform in different conditions of an experiment.

Counterbalancing

Suppose we used a repeated measures design in which all of the participants first learned words in “loud noise” and then learned them in “no noise.”

We expect the participants to learn better in “no noise” because of order effects, such as practice. However, a researcher can control for order effects using counterbalancing.

The sample would be split into two groups: experimental (A) and control (B).  For example, group 1 does ‘A’ then ‘B,’ and group 2 does ‘B’ then ‘A.’ This is to eliminate order effects.

Although order effects occur for each participant, they balance each other out in the results because they occur equally in both groups.

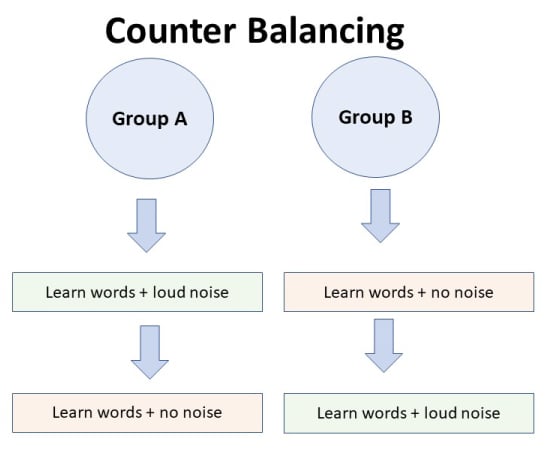
3. Matched Pairs Design

A matched pairs design is an experimental design where pairs of participants are matched in terms of key variables, such as age or socioeconomic status. One member of each pair is then placed into the experimental group and the other member into the control group .

One member of each matched pair must be randomly assigned to the experimental group and the other to the control group.

• Con : If one participant drops out, you lose 2 PPs’ data.
• Pro : Reduces participant variables because the researcher has tried to pair up the participants so that each condition has people with similar abilities and characteristics.
• Con : Very time-consuming trying to find closely matched pairs.
• Pro : It avoids order effects, so counterbalancing is not necessary.
• Con : Impossible to match people exactly unless they are identical twins!
• Control : Members of each pair should be randomly assigned to conditions. However, this does not solve all these problems.

Experimental design refers to how participants are allocated to an experiment’s different conditions (or IV levels). There are three types:

1. Independent measures / between-groups : Different participants are used in each condition of the independent variable.

2. Repeated measures /within groups : The same participants take part in each condition of the independent variable.

3. Matched pairs : Each condition uses different participants, but they are matched in terms of important characteristics, e.g., gender, age, intelligence, etc.

Learning Check

Read about each of the experiments below. For each experiment, identify (1) which experimental design was used; and (2) why the researcher might have used that design.

1 . To compare the effectiveness of two different types of therapy for depression, depressed patients were assigned to receive either cognitive therapy or behavior therapy for a 12-week period.

The researchers attempted to ensure that the patients in the two groups had similar severity of depressed symptoms by administering a standardized test of depression to each participant, then pairing them according to the severity of their symptoms.

2 . To assess the difference in reading comprehension between 7 and 9-year-olds, a researcher recruited each group from a local primary school. They were given the same passage of text to read and then asked a series of questions to assess their understanding.

3 . To assess the effectiveness of two different ways of teaching reading, a group of 5-year-olds was recruited from a primary school. Their level of reading ability was assessed, and then they were taught using scheme one for 20 weeks.

At the end of this period, their reading was reassessed, and a reading improvement score was calculated. They were then taught using scheme two for a further 20 weeks, and another reading improvement score for this period was calculated. The reading improvement scores for each child were then compared.

4 . To assess the effect of the organization on recall, a researcher randomly assigned student volunteers to two conditions.

Condition one attempted to recall a list of words that were organized into meaningful categories; condition two attempted to recall the same words, randomly grouped on the page.

Experiment Terminology

Ecological validity.

The degree to which an investigation represents real-life experiences.

Experimenter effects

These are the ways that the experimenter can accidentally influence the participant through their appearance or behavior.

Demand characteristics

The clues in an experiment lead the participants to think they know what the researcher is looking for (e.g., the experimenter’s body language).

Independent variable (IV)

The variable the experimenter manipulates (i.e., changes) is assumed to have a direct effect on the dependent variable.

Dependent variable (DV)

Variable the experimenter measures. This is the outcome (i.e., the result) of a study.

Extraneous variables (EV)

All variables which are not independent variables but could affect the results (DV) of the experiment. Extraneous variables should be controlled where possible.

Confounding variables

Variable(s) that have affected the results (DV), apart from the IV. A confounding variable could be an extraneous variable that has not been controlled.

Random Allocation

Randomly allocating participants to independent variable conditions means that all participants should have an equal chance of taking part in each condition.

The principle of random allocation is to avoid bias in how the experiment is carried out and limit the effects of participant variables.

Order effects

Changes in participants’ performance due to their repeating the same or similar test more than once. Examples of order effects include:

(i) practice effect: an improvement in performance on a task due to repetition, for example, because of familiarity with the task;

(ii) fatigue effect: a decrease in performance of a task due to repetition, for example, because of boredom or tiredness.

5.1 Experiment Basics

Learning objectives.

• Explain what an experiment is and recognize examples of studies that are experiments and studies that are not experiments.
• Distinguish between the manipulation of the independent variable and control of extraneous variables and explain the importance of each.
• Recognize examples of confounding variables and explain how they affect the internal validity of a study.

What Is an Experiment?

As we saw earlier in the book, an  experiment  is a type of study designed specifically to answer the question of whether there is a causal relationship between two variables. In other words, whether changes in an independent variable  cause  a change in a dependent variable. Experiments have two fundamental features. The first is that the researchers manipulate, or systematically vary, the level of the independent variable. The different levels of the independent variable are called conditions . For example, in Darley and Latané’s experiment, the independent variable was the number of witnesses that participants believed to be present. The researchers manipulated this independent variable by telling participants that there were either one, two, or five other students involved in the discussion, thereby creating three conditions. For a new researcher, it is easy to confuse  these terms by believing there are three independent variables in this situation: one, two, or five students involved in the discussion, but there is actually only one independent variable (number of witnesses) with three different levels or conditions (one, two or five students). The second fundamental feature of an experiment is that the researcher controls, or minimizes the variability in, variables other than the independent and dependent variable. These other variables are called extraneous variables . Darley and Latané tested all their participants in the same room, exposed them to the same emergency situation, and so on. They also randomly assigned their participants to conditions so that the three groups would be similar to each other to begin with. Notice that although the words  manipulation  and  control  have similar meanings in everyday language, researchers make a clear distinction between them. They manipulate  the independent variable by systematically changing its levels and control  other variables by holding them constant.

Manipulation of the Independent Variable

Again, to  manipulate  an independent variable means to change its level systematically so that different groups of participants are exposed to different levels of that variable, or the same group of participants is exposed to different levels at different times. For example, to see whether expressive writing affects people’s health, a researcher might instruct some participants to write about traumatic experiences and others to write about neutral experiences. As discussed earlier in this chapter, the different levels of the independent variable are referred to as  conditions , and researchers often give the conditions short descriptive names to make it easy to talk and write about them. In this case, the conditions might be called the “traumatic condition” and the “neutral condition.”

Notice that the manipulation of an independent variable must involve the active intervention of the researcher. Comparing groups of people who differ on the independent variable before the study begins is not the same as manipulating that variable. For example, a researcher who compares the health of people who already keep a journal with the health of people who do not keep a journal has not manipulated this variable and therefore has not conducted an experiment. This distinction  is important because groups that already differ in one way at the beginning of a study are likely to differ in other ways too. For example, people who choose to keep journals might also be more conscientious, more introverted, or less stressed than people who do not. Therefore, any observed difference between the two groups in terms of their health might have been caused by whether or not they keep a journal, or it might have been caused by any of the other differences between people who do and do not keep journals. Thus the active manipulation of the independent variable is crucial for eliminating potential alternative explanations for the results.

Of course, there are many situations in which the independent variable cannot be manipulated for practical or ethical reasons and therefore an experiment is not possible. For example, whether or not people have a significant early illness experience cannot be manipulated, making it impossible to conduct an experiment on the effect of early illness experiences on the development of hypochondriasis. This caveat does not mean it is impossible to study the relationship between early illness experiences and hypochondriasis—only that it must be done using nonexperimental approaches. We will discuss this type of methodology in detail later in the book.

Independent variables can be manipulated to create two conditions and experiments involving a single independent variable with two conditions is often referred to as a  single factor two-level design.  However, sometimes greater insights can be gained by adding more conditions to an experiment. When an experiment has one independent variable that is manipulated to produce more than two conditions it is referred to as a single factor multi level design.  So rather than comparing a condition in which there was one witness to a condition in which there were five witnesses (which would represent a single-factor two-level design), Darley and Latané’s used a single factor multi-level design, by manipulating the independent variable to produce three conditions (a one witness, a two witnesses, and a five witnesses condition).

Control of Extraneous Variables

As we have seen previously in the chapter, an  extraneous variable  is anything that varies in the context of a study other than the independent and dependent variables. In an experiment on the effect of expressive writing on health, for example, extraneous variables would include participant variables (individual differences) such as their writing ability, their diet, and their gender. They would also include situational or task variables such as the time of day when participants write, whether they write by hand or on a computer, and the weather. Extraneous variables pose a problem because many of them are likely to have some effect on the dependent variable. For example, participants’ health will be affected by many things other than whether or not they engage in expressive writing. This influencing factor can make it difficult to separate the effect of the independent variable from the effects of the extraneous variables, which is why it is important to  control  extraneous variables by holding them constant.

Extraneous Variables as “Noise”

Extraneous variables make it difficult to detect the effect of the independent variable in two ways. One is by adding variability or “noise” to the data. Imagine a simple experiment on the effect of mood (happy vs. sad) on the number of happy childhood events people are able to recall. Participants are put into a negative or positive mood (by showing them a happy or sad video clip) and then asked to recall as many happy childhood events as they can. The two leftmost columns of  Table 5.1 show what the data might look like if there were no extraneous variables and the number of happy childhood events participants recalled was affected only by their moods. Every participant in the happy mood condition recalled exactly four happy childhood events, and every participant in the sad mood condition recalled exactly three. The effect of mood here is quite obvious. In reality, however, the data would probably look more like those in the two rightmost columns of  Table 5.1 . Even in the happy mood condition, some participants would recall fewer happy memories because they have fewer to draw on, use less effective recall strategies, or are less motivated. And even in the sad mood condition, some participants would recall more happy childhood memories because they have more happy memories to draw on, they use more effective recall strategies, or they are more motivated. Although the mean difference between the two groups is the same as in the idealized data, this difference is much less obvious in the context of the greater variability in the data. Thus one reason researchers try to control extraneous variables is so their data look more like the idealized data in  Table 5.1 , which makes the effect of the independent variable easier to detect (although real data never look quite  that  good).

One way to control extraneous variables is to hold them constant. This technique can mean holding situation or task variables constant by testing all participants in the same location, giving them identical instructions, treating them in the same way, and so on. It can also mean holding participant variables constant. For example, many studies of language limit participants to right-handed people, who generally have their language areas isolated in their left cerebral hemispheres. Left-handed people are more likely to have their language areas isolated in their right cerebral hemispheres or distributed across both hemispheres, which can change the way they process language and thereby add noise to the data.

In principle, researchers can control extraneous variables by limiting participants to one very specific category of person, such as 20-year-old, heterosexual, female, right-handed psychology majors. The obvious downside to this approach is that it would lower the external validity of the study—in particular, the extent to which the results can be generalized beyond the people actually studied. For example, it might be unclear whether results obtained with a sample of younger heterosexual women would apply to older homosexual men. In many situations, the advantages of a diverse sample (increased external validity) outweigh the reduction in noise achieved by a homogeneous one.

Extraneous Variables as Confounding Variables

The second way that extraneous variables can make it difficult to detect the effect of the independent variable is by becoming confounding variables. A confounding variable  is an extraneous variable that differs on average across  levels of the independent variable (i.e., it is an extraneous variable that varies systematically with the independent variable). For example, in almost all experiments, participants’ intelligence quotients (IQs) will be an extraneous variable. But as long as there are participants with lower and higher IQs in each condition so that the average IQ is roughly equal across the conditions, then this variation is probably acceptable (and may even be desirable). What would be bad, however, would be for participants in one condition to have substantially lower IQs on average and participants in another condition to have substantially higher IQs on average. In this case, IQ would be a confounding variable.

To confound means to confuse , and this effect is exactly why confounding variables are undesirable. Because they differ systematically across conditions—just like the independent variable—they provide an alternative explanation for any observed difference in the dependent variable.  Figure 5.1  shows the results of a hypothetical study, in which participants in a positive mood condition scored higher on a memory task than participants in a negative mood condition. But if IQ is a confounding variable—with participants in the positive mood condition having higher IQs on average than participants in the negative mood condition—then it is unclear whether it was the positive moods or the higher IQs that caused participants in the first condition to score higher. One way to avoid confounding variables is by holding extraneous variables constant. For example, one could prevent IQ from becoming a confounding variable by limiting participants only to those with IQs of exactly 100. But this approach is not always desirable for reasons we have already discussed. A second and much more general approach—random assignment to conditions—will be discussed in detail shortly.

Figure 5.1 Hypothetical Results From a Study on the Effect of Mood on Memory. Because IQ also differs across conditions, it is a confounding variable.

Key Takeaways

• An experiment is a type of empirical study that features the manipulation of an independent variable, the measurement of a dependent variable, and control of extraneous variables.
• An extraneous variable is any variable other than the independent and dependent variables. A confound is an extraneous variable that varies systematically with the independent variable.
• Practice: List five variables that can be manipulated by the researcher in an experiment. List five variables that cannot be manipulated by the researcher in an experiment.
• Effect of parietal lobe damage on people’s ability to do basic arithmetic.
• Effect of being clinically depressed on the number of close friendships people have.
• Effect of group training on the social skills of teenagers with Asperger’s syndrome.
• Effect of paying people to take an IQ test on their performance on that test.

Share This Book

• Increase Font Size